Squares in Circles

The applet below illustrates Problem 5 from the 1959 International Mathematics Olympiad:

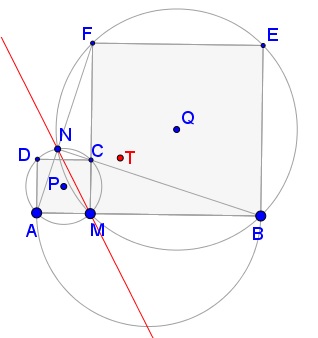
An arbitrary point $M\,$ is selected in the interior of the segment $AB.\,$ The squares $AMCD\,$ and $MBEF\,$ are constructed on the same side of $AB,\,$ with the segments $AM\,$ and $MB\,$ as their respective bases. The circles circumscribed about these squares, with centers $P\,$ and $Q;\,$ intersect at $M\,$ and also at another point $N.\,$ Let $N'\,$ denote the point of intersection of the straight lines $AF\,$ and $BC.\,$

Prove that the points $N\,$ and $N'\,$ coincide.
Prove that the straight lines $MN\,$ pass through a fixed point $S\,$ independent of the choice of $M.$
Find the locus of the midpoints of the segments $PQ\,$ as $M\,$ varies between $A\,$ and $B.$

Created with GeoGebra

Solution

Prove that the points $N\,$ and $N'\,$ coincide.
Prove that the straight lines $MN\,$ pass through a fixed point $S\,$ independent of the choice of $M.$
Find the locus of the midpoints of the segments $PQ\,$ as $M\,$ varies between $A\,$ and $B.$

Problem 5 from IMO 1959, illustration

Solution

Let $P\,$ and $Q\,$ be the centers of squares $AMCD\,$ and $MBEF\,$ and $(P)\,$ and $(Q)\,$ the circumscribed circles.

Triangles $ABN'\,$ and $CBM\,$ are right and similar. Their corresponding legs are at right angles; therefore, so are the hypotenuses: $AN' \perp BC.\,$ Since $\angle AN'C\,$ is right and $AC\,$ is the diameter of $(P),\,$ $N'\,$ lies on that circle. Similarly, $N'\,$ lies on $(Q),\,$ implying $N' = N.\,$

In $(P),\,$ $\angle ANM\,$ subtends a quarter circle. Thus $\angle ANM = 45^{\circ}.\,$ Similarly, in $(Q)\,$ $\angle BNM = 45^{\circ}.\,$ As we just saw, $\angle ANB = 90^{\circ}\,$, implying that $MN\,$ is the bisector of the angle at $N.\,$ $MN,\,$ therefore, passes through the lowest point of the circle with $AB\,$ as a diameter, proving #2.

Let $T\,$ be the midpoint of $PQ,\,$ $P_{0}\,$ and $Q_{0}\,$ projections on $AB\,$ of $P\,$ and $Q,\,$ respectively. $P_{0}\,$ is the midpoint of $AM,\,$ $Q_{0}\,$ the midpoint of $BM.\,$ $P\,$ lies on the diagonal $AC\,$ of square $AMCD,\,$ $Q\,$ on the diagonal $BF\,$ of square $MBEF.\,$ It follows that $AP_{0} = PP_{0}\,$ and $BQ_{0} = QQ_{0}\,$ from which

$PP_{0} + QQ_{0} = AP_{0} + BQ_{0} = \displaystyle \frac{AB}{2}.$

The height of the midpoint $T\,$ of $PQ\,$ is the average of $PP_{0}\,$ and $QQ_{0}\,$ which is $\displaystyle \frac{AB}{4},\,$ independent of $M.\,$ Thus if $P'\,$ and $Q'\,$ are at the distance $\displaystyle \frac{AB}{4}\,$ from $AB\,$ and lie on the diagonals of the two squares, $T\,$ ranges over $P'Q'.\,$ However, note that if $M\,$ moves outside $AB\,$ and one of the length $AM\,$ or $BM\,$ becomes negative, with the corresponding square is drawn on the other side of $AB,\,$ $T\,$ still belongs to the line $P'Q'\,$ but is no longer located inside the segment $P'Q'.$

The problem's configuration exhibits additional properties. For example, if $U\,$ denotes the point of intersection of the two diagonals, then the circle with $PQ\,$ as diameter passes through $M\,$ and $U.$

Note: Part 1 of the problem has been included as #367 in the collection by Barbeau et al.

References

E. J. Barbeau, M. S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges, MAA, 1995.

71547473