A Triangle of Antreas Hatzipolakis

This applet requires Sun's Java VM 2 which your browser may perceive as a popup. Which it is not. If you want to see the applet work, visit Sun's website at https://www.java.com/en/download/index.jsp, download and install Java VM and enjoy the applet.

What if applet does not run?

In ΔABC, D, E, F are the midpoints of sides BC, AC, and AB, while X, Y, Z are the points of tangency of the incircle with those sides. Let M be the foot of the perpendicular from A to BI and N the foot of the perpendicular from A to CI. Then

Points M, N, E, F are collinear,
Points X, Y, M are collinear, as are the points X, Z, N.

Proof

By the construction, ΔABM is right with ∠AMB = 90°, implying

AF = BF = FM.

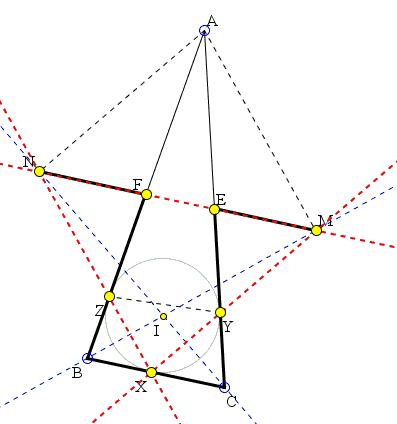
Hatzipolakis Triangle

It follows that ΔBFM is isosceles and ∠FBM = ∠FMB. Thus the sum of these angles equals ∠AFM. On the other hand, since BI bisects ∠ABC, the sum of equal angles FBM and CBM equals ∠ABC. We see that

∠AFM = ∠ABC

so that FM||BC and, since F is the midpoint of AB, FM is a midline in ΔABC and passes through another midpoint, viz., E. This shows that M lies on EF. By symmetry the same holds for N.

Further

	EM	= FM - EF
		= AF - EF
		= AB/2 - BC/2
		= (AB - BC)/2
		= (AZ - CX)/2
		= (AY - CY)/2
		= (AC - 2·CY)/2
		= (2·EC - 2·CY)/2
		= EC - CY
		= EY,

implying that ΔMEY is isosceles: EM = EY. In addition, ∠XCE = ∠CEM wherefrom ∠XYC = ∠EYM making therm vertical and XYM a straight line. XZN is treated similarly.

Michel Cabart came up with a different proof:

Consider point D of intersection of lines AM and BC. Then

M is middle of AD thus belongs to EF
by symmetry XD = ZA = YA thus XC·YA·MD = XD·YC·MA and M belongs to line XY by Menelaus' theorem applied to triangle ACD.

(Triangle AMN along with two other triangles similarly constructed at vertices B and C have several engaging properties first observed by Antreas Hatzipolakis which explains the attribution in the title.)

References

Jan Vonk, On the Nagel Line and a Prolific Polar Triangle, Forum Geometricorum Volume 8 (2008) 183-196

71950110