Triangle Construction from Angle, Altitude and Median

The applet below illustrates construction of a triangle, given ∠BAC (= α), altitude AH (= h), and median AM (= m).

(Slides are draggable. Use the three on the left to setup the problem, the one on the right to determine the solution.)

Solution

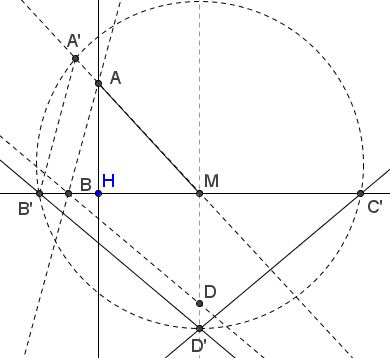
triangle construction from A, h,M

Start with constructing ΔHAM and a line perpendicular to HM at M. On that line choose an arbitrary point D' and find points B', C' on HM such that ∠MD'B' = ∠MD'C' = 90° - α/2.

Let the circumcircle of ΔB'C'D' meet line AM at point A' on the side of B'. Join A'B' and draw AB||A'B'. B is another vertex of the sought ΔABC.

The solution is explained by the fact that all triangles B'D'M, the circumcircles of ΔB'C'D', point A' are homothetic from M such that all A'B' are parallel to each other and to the "right" one AB, and similarly for B'D'||BD.