Square from Four Points, One on Each Side
Here's a problem from an old Russian problem collection by D. O. Shklyarsky, N. N. Chentsov, Y. M. Yaglom Selected Problems and Theorems from Elementary Mathematics, Part 2 (Planimetry) (1952, #70):
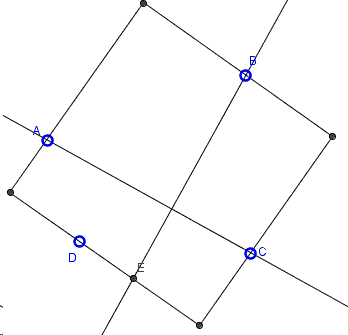
There are four points in the plane. Construct
- a square
- a rectangle, with a given ratio of the sides
- a rhombus, with a given acute angle
such that each side (or its extension) would pass through exactly one of the given points.
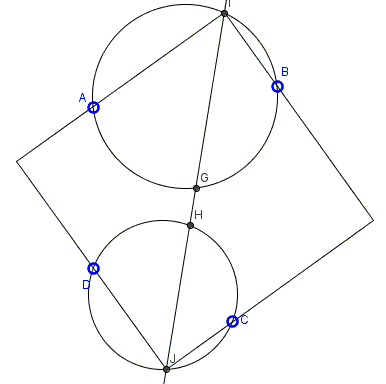
Part (a) comes with two constructions, the first is naturally extended to solve Part (b), the second extends to solve Part (c).
In general, Part (a) may have 6 or infinitely many solutions, Parts (b) and (c) - 12.
The problems in the book have been previously used at the Moscow University Math Circle and are considered non-standard, meaning that they require the kind of thinking not advanced in the school curricula, but which is customary in the contemporary mathematics. This particular problem is not marked as especially difficult.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73573069