A Diameter As a Diagonal of Inscribed Quadrilateral

Here's a problem from an old Russian problem collection:

Assume that in a cyclic quadrilateral one of the diagonals coincides with a diameter of the circumscribed circle.

a problem for cyclic quadrilateral when a diagonal serves a diameter

Prove that the projections of the opposite sides on the other diagonal are equal.

The applet below illustrates the problem and two solutions:

Proofs

Proof 1

Refer to the following diagram.

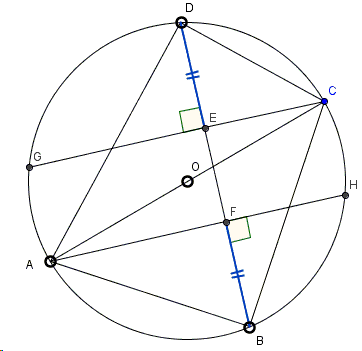
a problem for cyclic quadrilateral when a diagonal serves a diameter - solution 1

Extend the perpendiculars AF and CE to a second intersection with the circle in points H and G, respectively. Lines AH and CG are parallel and, emanating from the two ends of a diameter, are, therefore, equal - by symmetry. BF and DE are two perpendiculars to equal chords CG and AH and area, therefore, equal - again by symmetry (in this case one may claim "by paper folding".)

Proof 2

Drop a perpendicular OP from the center O of the circle to BD.

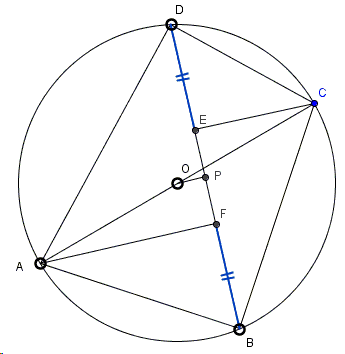
a problem for cyclic quadrilateral when a diagonal serves a diameter - solution 2

P is the midpoint of BD: BP = DP. Since AO = CO, their projections on BD are equal: EP = FP. Subtracting gives

DE = DP - EP = BP - FP = BF.

71220285