PLL: Apollonius' Problem with Two Lines and a Point
Below I give an Euclidean construction to a variant of the Problem of Apollonius:
Find a circle through a given point \(D\) and tangent to two given lines \(AB\) and \(AC\):
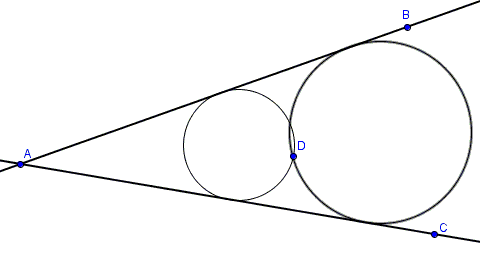
(The applet below illustrates the proof. Points \(A, B,C,D\) are draggable. This permits changing the configuration, but within certain limitations.)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Construction
Find a circle through a given point \(D\) and tangent to two given lines \(AB\) and \(AC\):

All circles inscribed in angle \(BAC\) are homothetic with center at \(A\). I shall designate such circles by their center: let \((E)\) be one of these. The circle(s) we are looking for is homothetic to \((E)\) and passes through point \(D\).
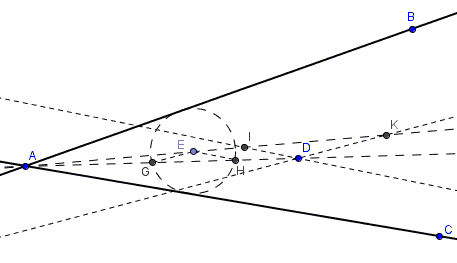
The image of point \(D\) in the inverse homothety lies on \(AD\) at the intersection of the latter with \((E)\). Unless \(D\), lies on one of the given lines, there are two intersection points: \(G\) and \(H\). The homothetic image of \(EG\) is \(DK\), with \(K\) on the bisector of \(\angle BAC\) and \(DK||EG\). The homothetic image of \(EH\) is \(DI\), with \(I\) on the bisector of \(\angle BAC\) and \(DI||EH\). Points \(I\) and \(K\) serve as centers of two solutions to the problem.
In case where the two given lines are parallel. All circles touching the two are equal, and the problem is solved with translation, instead of homothety. Again, unless the given point lies on one of the given lines, there are two solutions. If it does, the solution is unique.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73614988
