Rhombus in Circles
The problem below was posted posted at the CutTheKnotMath facebook page by Cõ Gẫng Lên:
Segments \(AB\) and \(CD\) are equal. Lines \(AB\) and \(CD\) intersect at \(M.\) Form four circumcircles: \((E)=(ACM),\) \((F)=(ADM),\) \((G)=(BDM),\) \((H)=(BCM).\)
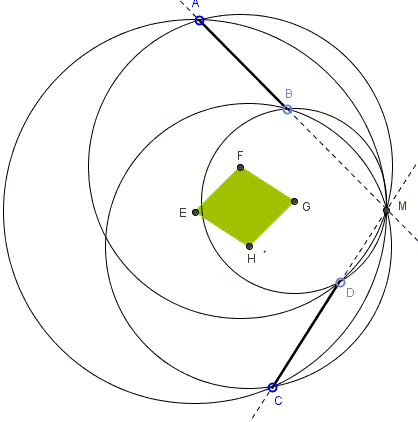
Prove that points \(E,F,G,H\) form a rhombus, with \(\angle EFG=\angle AMC\).
(The applet below illustrates the problem.)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
Segments \(AB\) and \(CD\) are equal. Lines \(AB\) and \(CD\) intersect at \(M.\) Form four circumcircles: \((E)=(ACM),\) \((F)=(ADM),\) \((G)=(BDM),\) \((H)=(BCM).\)

Prove that points \(E,F,G,H\) form a rhombus, with \(\angle EFG=\angle AMC\).
Solution
It pays to produce perpendicular bisectors of \(AM,BM,CM,DM.\) This are the lines that form the quadrilateral \(EFGH.\)
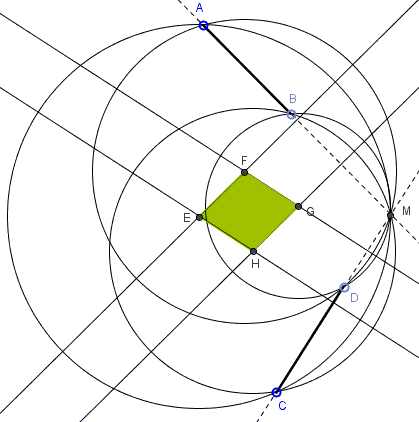
The lines come in parallel pairs with distances between the lines within the pairs equal to, say, \(AB/2.\) This why we get a rhombus. The sides of \(\angle EFG\) are perpendicular to those of \(\angle AMC,\) and this is why the two are equal.
This is a nice simple configuration. The shape or size of rhombus \(EFGH\) does not depend on the relative position of the two given segments, but only on their length and the angles they form. If they are orthogonal, the rhobus becomes a square. If the angle between them is \(60^{\circ},\) the rhombus consists of two equilateral triangles \(EFG\) and \(EHG;\) to construct either one only needs to draw three of the four circles.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73554858
