Five Squares in Complex Numbers

The problem below was posted at the CutTheKnotMath facebook page by Cõ Gẫng Lên. To simplify the diagram I do not name the many corners and most other points. This makes the formulation of the problem somewhat verbose.

Four squares each share a corner with a fifth square, as shown below

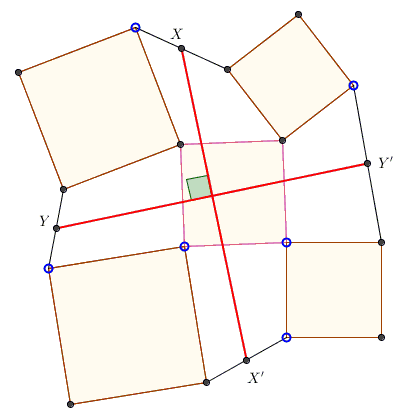
Five Squares Problem - problem

As seen, the neighboring corners of the adjacent squares are joined, and the midpoints - $X,Y,X',Y'$ - of the so obtained segments are marked. Prove that the segments $XX'$ and $YY'$ are equal and perpendicular.

(The applet below illustrates the problem.)

Solution

Four squares each share a corner with a fifth square, as shown below

Five Squares Problem - problem

Solution

A solution of the problem in complex numbers is straightforward. Let's place the origin at the center of the square and denote the four halves of its diagonals $x,xi,-x,-xi.$

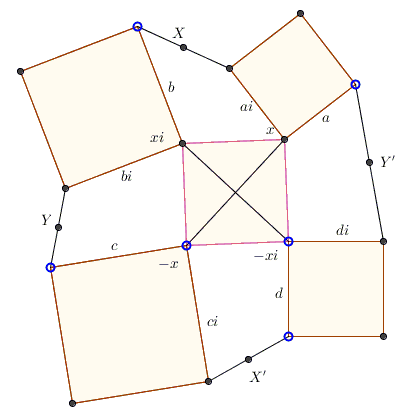
Five Squares Problem - solution

The four attached squares are formed by the pairs $a,ai,$ $b,bi,$ $c,ci,$ and $d,di,$ which allows finding expressions for the midpoints:

$ \begin{align} 2X &= x+ai+xi+b \\ 2Y &= xi + bi - x + c \\ 2X' &= -x +ci - xi + d \\ 2Y' &= -xi + di + x + a. \end{align} $

From here,

$ \begin{align} 2(X - X') &= 2x + 2xi + b-d + ai - ci \\ 2(Y - Y') &= 2xi-2x+c-a+bi-di \\ &= i[(2x+2xi)+i(b-d)+i(ai-ci)] \\ &= i\cdot 2(X-X'). \end{align} $

Which shows that $XX'= X'-X$ and $YY'=Y'-Y$ are obtained from each other by a rotation through $90^{\circ}.$

71543677