Problem 4 from the 1959 IMO: Construction of a Right Triangle
Here's a problem from an old Russian problem collection:
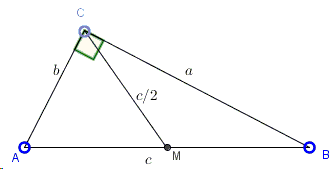
Construct a right-angled triangle whose hypotenuse \(c\) is given if it is known that the median from the right angle equals the geometric mean of the remaining two sides of the triangles.
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
The applet below illustrates the problem and a solution:
The solution is based on the observation that the triangles \(ABC\) and \(CBD\) are similar, implying the proportion \(\displaystyle\frac{b}{c}=\frac{h}{a}\). The solution further makes use of the fact that in a right triangle the midpoint of the hypotenuse serves as the circumcenter so that the median from the right angle equals half of the hypotenuse. The construction is then obvious: draw a line parallel to the hypotenuse at distance \(c/4\) from it. The two points where that line intersects the semicircle with \(AB\) as diameter are sought locations of vertex \(C\).
The original solution [The IMO Compendium, p357-358] went in a somewhat different way:
By the Pythagorean theorem \(c^{2}=a^{2}+b^{2}\) which, together with \(c/2=\sqrt{ab}\), implies \(a+b=c\sqrt{3/2}\). Given a desired \(\Delta ABC\), let \(D\) be a point on \(AC\) such that \(CD=CB\). In that case, \(AD=a+b=c\sqrt{3/2}\), and also \(\angle ADB=45^{\circ}\), because \(BC=CD\).
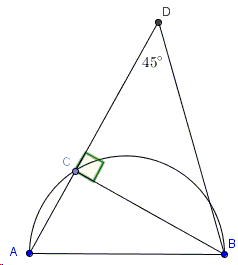
With this analysis in mind, measure \(AD=c\sqrt{3/2}\) and draw a ray \(DX\) such that \(\angle ADX=45^{\circ}\). Next, construct circle \(C(A,c)\) with center \(A\) and radius \(c\). Take \(B\) to be the point of intersection of the circle and \(DX\) and drop a perpendicular \(BC\) to \(AD\).
References
- D. Djukic et al, The IMO Compendium, Springer, 2011 (Second edition)
|Contact| |Front page| |Content| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
73561414
