A Geometry Problem from 2012 IMO - Problem 5

The applet below illustrates Problem 5 from the 2012 IMO:

Let ABC be a triangle with ∠BCA = 90°, and let D be the foot of the altitude from C. Let X be a point in the interior of the segment CD. Let K be the point on the segment AX such that BK = BC. Similarly, let L be the point on the segment BX such that AL = AC. Let M be the point of intersection of AL and BK.

Show that MK = ML.

Solution

The Euclidean construction (i.e., with compass and ruler) of the problem configuration suggests a few extra elements. First of all, there is circle C(A, AC) - centered at A with radius AC - that intersects BX in L. Similarly, there is circle C(B, BC) that intersects AX in K. The altitude CD serves as the radical axis of the two circles.

The tangent to C(A, AC) at L and the tangent to C(B, BC) at K intersect in E. If we can show that E lies on the radical axis CD, the problem will be solved because then, EK = EL and since AL⊥EL and BK⊥EK, right triangles EKM and ELM are equal, making MK = ML, as required.

Let E' be the point of intersection of CD and EL. Since angles ADE' and ALE' are right, the four points A, D, L, E' are concyclic. As inscribed angles subtended by the same chord, ∠AE'D = ∠ALD. In right ΔABC, AC/AD = AB/AC; by construction then AL/AD = AB/AL. For this reason and because they share the angle at A, triangles ALD and ABL are similar, implying that ∠LBA = ∠ALD. Combining what we found so far,

∠XBD = ∠LBA = ∠ALD = ∠AE'D.

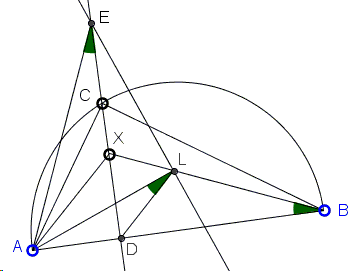
A step in the solution of problem 5 IMO 2012

It follows that the right triangles AE'D and DBX are similar, so that DE'/AD = BD/DX, or DE' = AD·BD/DX, which shows that E' depends solely on A, B, D, and X. If we set E'' to be the intersection of AK and CD, we shall similarly arrive at DE'' = AD·BD/DX, showing that E' = E'' = E, and we are done.

(A different solution can be found at the IMO site.)

72654923