A problem with equilateral triangles: What is it?
|
| Buy this applet What if applet does not run? |
The applet suggests the following problem: Let there be three equal equilateral triangles each with one vertex at the center of a circle and the other two on its circumference. Denote the vertices on the circumference as A1, B1, A2, B2, and A3, B3. Let M1 be the midpoint of B1A2, M2 the midpoint of B2A3, and M3 the midpoint of B3A1. Prove that the triangle M1M2M3 is also equilateral.
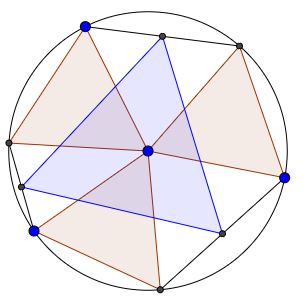
I'll use complex numbers and the criteria from Connes' proof of Morley's theorem.
Assume that the center of the circle lies at the origin. Borrowing notations from that page, the fact that the three triangles are equilateral is then expressed as
| (1) | Ai + jBi = 0, i = 1, 2, 3 |
M1 = (B1 + A2)/2, etc. To prove that the triangle in question is equilateral suffice it to show that
| (2) | M1 + jM2 + j2M3 = 0, |
or
| (3) | (B1 + A2) + j(B2 + A3) + j2(B3 + A1) = 0. |
All it takes to see that this is indeed so is a substitution from (1):
| (4) | B1 - jB2 + jB2 - j2B3 + j2B3 - j3B1 = 0, |
but j3 = 1, which concludes the proof.
Remark
We have proved more than we set out to. Indeed, the proof only depends on (1), i.e. on the fact that the three triangles are equilateral. We never used the condition that 6 vertices of those triangles lie on a circle.
| Buy this applet What if applet does not run? |
An extension of this proof could be found elsewhere.
Remark
The same method proves a further generalization of the theorem. Above, three equilateral triangles have shared a vertex (the one assumed to coincide with the origin). We may split that point into three provided they form another equilateral triangle. More accurately, replace (1) with
| (1') | Ai + jBi + j2Ci = 0, i = 1, 2, 3 |
and add a condition binding vertices C into an equilateral triangle:
| (5) | C1 + jC2 + j2C3 = 0. |
(3) remains valid, but its derivation (4) should be modified ever so lightly to produce (2).
Remark
As has been reported by Martin Gardner in his article The Asymmetric Propeller that appeared in The College Mathematics Journal, v. 30, n. 1, 1999 (18-22), an even more general result has been proved by Leon Bankoff. The four triangles in question must not be equilateral at all! If all four are similar, then the corresponding midpoints form a fifth triangle of the same shape, i.e. similar to the given four. The above method of proof however meets here its limitation. A different technique shows that even in a more general situation complex numbers can do a wonderful job.
The problem has been included in the 28th (1967) Putnam Competition (B1) in the following form:
A hexagon is inscribed in a circle radius 1. Alternate sides have length 1. Show that the midpoints of the other three sides form an equilateral triangle.
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 40620297 |
