The Cleaver: What is this about?
A Mathematical Droodle

---

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

---

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet may suggest the following statment:

In ΔABC, let CL be the angle bisector of angle C, M the midpoint of AB, and MD||CL. (D lies on the longest of AC and BC.) Then points M and D split the perimeter of ΔABC into equal halves.

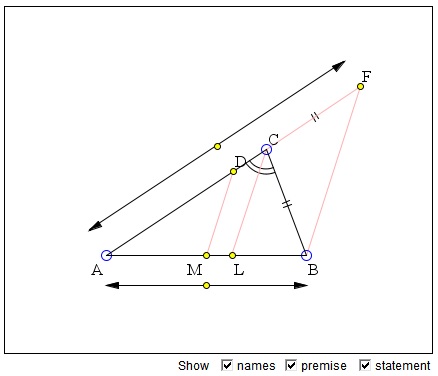
Assume AC > BC. Extend AC beyond C to F such that, BC = CF and, consequently, AF = AC + BC. Further, ΔBCF is isosceles, its angle bisector at C is perpendicular to the base BF. On the other hand, it is also perpendicular to the external angle bisector, i.e. CL, from which CL||BF. Since M is the midpoint of AB and MD||CL, we also have MD||BF, which implies that D is the midpoint of AF in ΔAFB:

AD = BC + CD.

By construction,

AM + BM,

so that

AM + AD = BM + BC + CD.

The line MD that joins a midpoint of a side with the opposite perimeter-bisecting point is called a cleaver. The three cleavers in a triangle intersect at the Spieker center of the triangle.

References

1. R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995, pp. 2-4

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny