A Chain of Touching Circles in a Polygon |
| Buy this applet What if applet does not run? |
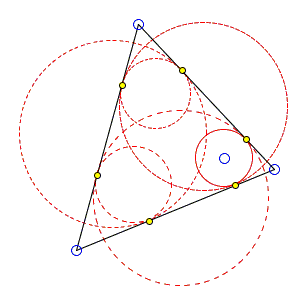
The applet illustrates an extension of a 6 circles theorem due to Bui Quang Tuan from triangles to convex polygons with more than 3 sides.
Given a convex n-gon A1A2...An (n ≥ 3 and odd), start with inscribing a circle C1 into ∠A3A1A2 and note point T12 of tangency on the side A1A2. Next inscribe circle C2 into ∠A1A2A3 so that it is tangent to A1A2 at T12 and note point T23 of tangency with side A2A3. Continue inscribing circles C3, C4, C5, and so on, into successive angles. Then C2n = C1.
For regular polygons, the length of the chain may be 1 or 2N.
The situation appears to be analogous to an extension of another 6 circles theorem.
(The applet can emphasize successive pairs of circles counting from 0 to
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny| 41143704 |
