Angles in a Cube I

What Is That About?

angle of 60 between two diagonals of a cube

Try again

Problem

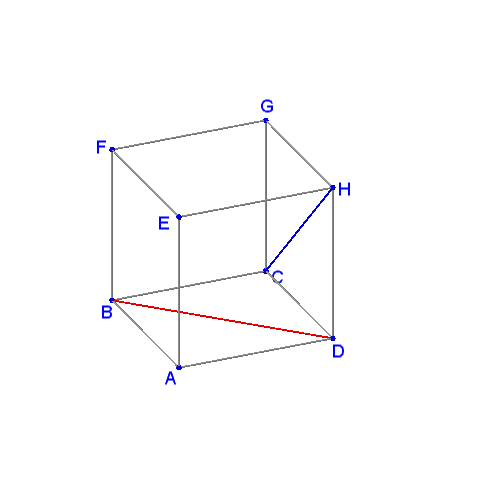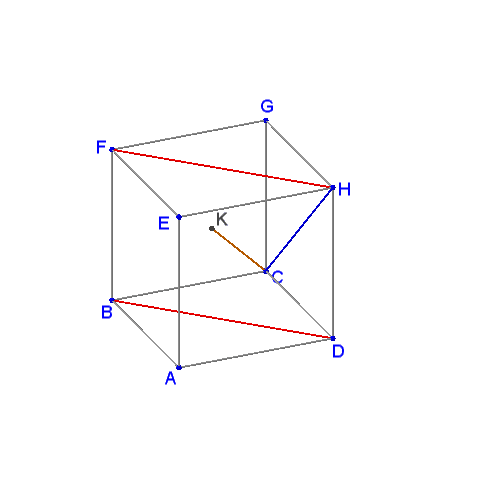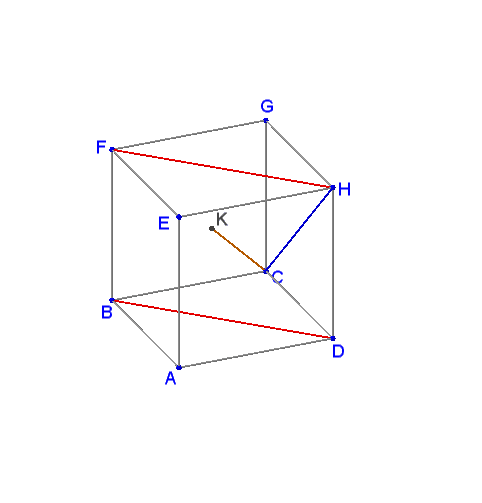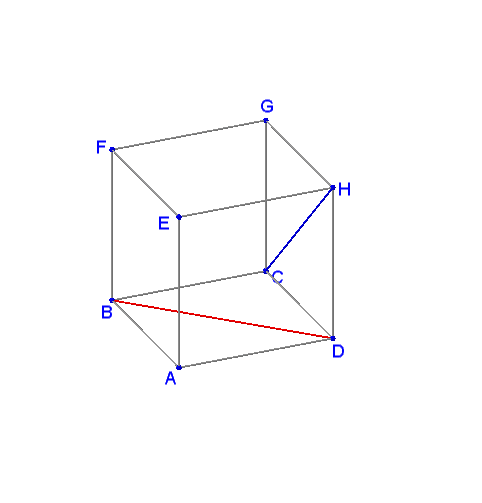
Let denote the vertices of a cube $ABCD$ (for the bottom face) and $EFGH$ (for the top face), with $E$ above $A,$ etc.

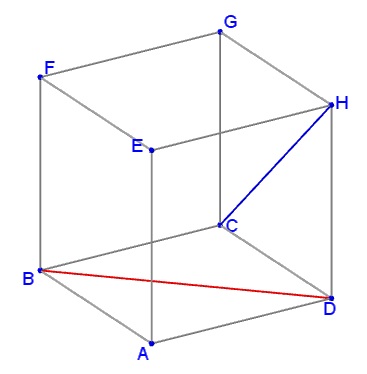
angle of 60 between two diagonals of a cube,illustration

What is the angle between two lines, $CH$ and $BD?$

Solution

Start with drawing $HF\parallel BD.$ $\widehat{(BD,CH)}=\widehat{(HF,CH)}.$ Add $CH.$

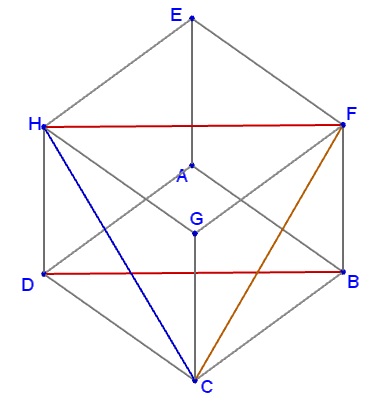
angle of 60 between two diagonals of a cube, solution

Now observe that $HF=CF=CH$ as all three are the diagonals of the faces of a cube. Thus $\Delta BCH$ is equilateral and $\angle CFH=\widehat{(HF,CH)}=60^{\circ}.$ It follows that $\widehat{(BD,CH)}=60^{\circ}.$


Related material
Read more...

  • Angles in a Cube II
  • Angles in a Cube III
  • Bimedians in a Regular Tetrahedron
  • Cut the Cone
  • Cut the Cube
  • Cut the Cylinder

    • |Activities| |Contact| |Front page| |Contents| |Geometry|

    Copyright © 1996-2018 Alexander Bogomolny

    72199768