Geometric view of the Sieve of Eratosthenes

YouTube fast becomes a means of spreading math wonders. I was recently advised of a video posted at YouTube by Javier Torres Suárez. The video presents a step-by-step selection of dots in a triangular grid in such a manner that, wonderfully, the only rows of the grid that remain unchanged correspond to prime numbers.

The applet below provides an interactive simulation for the process. There is also extra functionality that may help explain the phenomenon.

The whole applet area clickable. The effect of pressing the left button while the cursor hovers over a dot depends on the combination of the three check boxes: descendants, ancestors, siblings. The meaning of the terms will be explained shortly. Pressing the button while the cursor is outside of the dots shows a triangular frame underlying a single step in the process associated with the row in which the button has been pressed.

The applet displays the final configuration obtained by the process of marking. Each step my be observed by clicking outside of any dot, as mentioned in the previous paragraph. Also, the inner dot markings can be Cleared and the process recommenced with the One step button.

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

Geometric view of the Sieve of Eratosthenes

What if applet does not run?

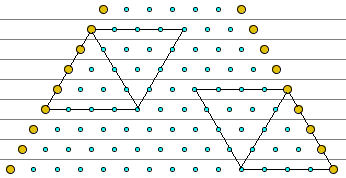
In the original video the process starts with an grid in which only the border dots are marked. On each step of the process a row is selected. That row is rotated 60° clockwise around its left end point and counterclockwise around its right end point. The row and its two rotations form an (upside down) equilateral triangle in which the legs inherit the dot configuration from the base. The process begins with row #2.

Dots in the grid may be affected by the dots above them. Thus a dot has a sequence of ancestors whose markings it receives. Each marked dot also passes the markings on to some dots - the descendants - below. Finally, some dots in a row are called siblings for a reason that will soon become clear.

To gain an insight into the workings of the algorithm, let's assign to each dot a pair of indices (r, k) - the coordinates - that uniquely determines the location of the dot in the triangle. The first coordinate is the row number (starting with row 0) in which the dot is located; the second coordinate indicates the position of the dot in the row starting with 0 for the leftmost dot.

The rotation of row #r around its left end point moves dot (r, k) to the position (r + k, k):

(R)	L(r, k) = (r + k, k).

This is because the dots (r, 0), (r, k), (r + k, 0), and (r + k, k), for example, form a rhombus that consists of two equilateral triangles with vertices (r, 0), (r, k), (r + k, k) and (r, 0), (r + k, 0), (r + k, k).

The counterclockwise rotation around the dot (r, r) is described by:

(L)	R(r, k) = (r + (r - k), r) = (2r - k, r).

This is because the dots (r, k), (r, r), (2r - k, 2r - k), and (2r - k, r) form a rhombus that consists of two equilateral triangles with vertices (r, k), (r, r), (2r - k, r) and (r, r), (2r - k, 2r - k), (2r - k, r).

It may be worth noting that the lines parallel to the edges of the grid have the equations

{(r, k): k = const} and
{(r, k): r - k = const},

with the left and right edge being {(r, 0)} and {(r, r)}, respectively.

One important property of the operators L and R is that they preserve the GCD - the greatest common divisor of the two components. Indeed,

GCD(r, k) = GCD(r + k, k) and
GCD(r, k) = GCD(r - k, r) and so also
GCD(r, k) = GCD(2r - k, r).

The ancestor operators are the inverses of L and R:

L^-1(r, k) = (r - k, k) and
R^-1(r, k) = (k, 2k - r).

So ancestors and descendants of a dot share the same GCD. The range of operator L^-1 is

S_L = {(r, k): r - k ≥ k) = {(r, k): r ≥ 2k).

That of R^-1 is given by

S_R = {(r, k): 0 ≤ 2k - r ≤ k) = {(r, k): k ≤ r ≤ 2k}.

The union of the two is the entire grid:

S_R ∪ S_R = {(r, k): k ≤ r}.

It would follow that all the dots on the grid have ancestors. The dots on the two edges have been marked from the outset and are thus of not interest. In particular, the three top dots - (0, 0), (0, 1), (1, 0) - are dropped from consideration. This is why in fact we have started from the row #2. Other than that there are no limitations: all other dots have ancestors. We are interested in finding the topmost progenitor(s) of a given dot (r, k). Let's designate the set of top progenitors T(r, k). We have the following

Theorem

Let g = GCD(r, k). Then

if g > 1, T(r, k) = { (0, g), (g, g) },
if g = 1, T(r, k) = { (2, 1) }.

Proof

The left ancestor operator L^-1 applies to a dot (r, k) whenever k ≤ r/2. The right ancestor operator R^-1 applies whenever k ≥ r/2. Each produces a dot above (r, k) but with the same GCD. Assume that applying either operator repeatedly we reached a top dot (s, t) with GCD(s, t) = g, but s ≠ 0 and s ≠ t.

In case where g = 1, we will be able to move further up unless (s, t) = (2, 1). In case g > 1 a further move possible unless either (s, t) = (0, g) or (s, t) = (g, g). The only dot whose ancestor is one of these is (2g, g). But this one has both (0, g) and (g, g) as ancestors.

What this statement shows is that the dots (r, k), with mutually prime r and k, remain unmarked. In particular, the dots in the rows with prime r remain unmarked, so that those rows remain unchanged.

We define also siblings as the dots in a single row that have the same GCD. In practice this means that siblings come in the form

(r, nd), n = 0, 1, ...

where d is a divisor of r. The term seems natural but is not quite appropriate because the relation of being siblings in this sense is not transitive. For example in row 12 there are four groups of siblings. These are defined by GCD's equal to 2, 3, 4, 6. The dot (12, 6) belongs to three groups, biz., those with GCD 2, 3, 6 of which the first two have unrelated elements, e.g., (12, 2) and (12, 3) which are both siblings of (12, 6) are unrelated nonetheless.

The whole process is the Sieve of Eratosthenes in disguise. To see this imagine a modified process wherein we first apply the reflection steps to the even numbered rows, then to the rows with numbers divisible by 3, then those divisible by 5 and so on. The result will be exactly the same, except most of the marked dots will have been marked repeatedly.

Related material Read more...
	Sieves


	Listing All the Composite Numbers
	Lucky Numbers
	Sieve of Eratosthenes
	Sieve of Squares
	The Parabolic Sieve of Prime Numbers

71927503