Solution to the 4 Travelers problem

Miguel Branchtein, Brasil
July 27, 2003

Here's another solution to the 4 travelers' problem.

We draw the four straight lines where travelers 1, 2, 3 and 4 respectively travel. Their meeting points are A, B, C, D, E and F.

Given that they meet in A, B, C, D and E, we must show that they also meet in F.

The straight line FG is just an auxiliary line, drawn from F paralel to line 1. The point where it crosses line 2, we'll call it G.

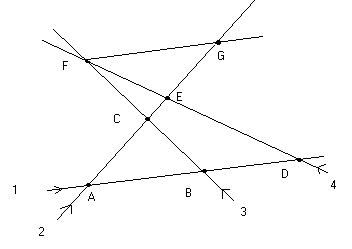
We call    the distance between points A and B, and so forth. We call V₁ the speed of traveler 1, and so forth.

From triangle ABC, we see that, in order that travelers 2 and 3 meet in point C, in the same time traveler 2 goes from A to C, traveler 1 must go from A to B, and then traveler 3 goes from B to C. That is,

(1)

Similarly, from triangle ADE, we have

(2)

At last, from triangle CEF, we get

(3)

Given (1) and (2), we have to prove (3).

We substitute 1/V₃, from (1), and 1/V₄ , from (2), into (3).

Putting together all terms in 1/V₁ and 1/V₂

(4)

In order to evaluate these, we observe that triangle GFC is similar to triangle ABC:

And triangle GFE is similar to triangle ADE:

Substituting these relations in (4), we get

or

proving eq. (4), and consequently eq. (3).