The many ways to construct a triangle II

h_c, l_c, m_c

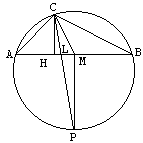
Assume the triangle ABC is given and draw its circumcircle. Draw also h_c, l_c, m_c. Extend l_c to the intersection with the circle at P and connect M_c (I'll write M for simplicity. The same convention applies to L_c and H_c.) Since P is the midpoint of the arc APB and M is the midpoint of AB, MP is perpendicular to AB and, therefore, is parallel to CH. We conclude that CP (the bisector of C) lies between CH and MP. Finally, the foot of the angle bisector L lies between H and M. This is universally true for every triangle.

The center of the circle lies on MP and on the perpendicular bisector of CP. From here we get the following construction:

Form a right triangle CHM. With the center at C sweep an arc of radius l_c. If it does not intersect HM between H and M, the construction is not possible. Otherwise we get a point L. Continue CL beyond L and draw a perpendicular to HM at M. The two lines are bound to intersect at P. Draw a perpendicular bisector of CP till it intersects MP at O. With the radius OP draw a circle with center O. Extend HM both directions to obtain A and B.
a, b, A

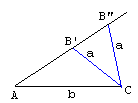
This is a well known construction and, in principle, the three elements a, b, and A may not define a triangle or may not define it uniquely. When the angle is right the triangle is defined in a unique way.

Draw AC of the given length b and the angle A. The circle of radius a and centered at C may intersect the other leg of A either at two points B', B", at one point B (it will actually touch AB) or not at all. When the point of intersection is unique the angle B is right. If this is known in advance, we may use a different approach.

If B is right, AC is the hypotenuse of the triangle ABC. Its midpoint serves as the circumcenter of the triangle. Draw AC and a circle with diameter AC. From C draw an arc with radius a.
h_a, b, c

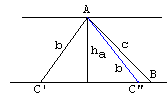
Draw two parallel lines h_a (units) apart. Pick a point A on one of them and from this point and with the center at A draw arcs of radii a and b till they intersect the other line. The problem may have no solution (e.g., b<h_a or b<h_a). Otherwise, it may have one solution (b=h_a or c=h_a). And lastly, it may have two solutions ABC' and ABC" as indicated in the diagram.
aa, H_b, H_c
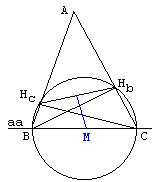
Triangles BH_bC and BH_cC are both right. Therefore, the two given points H_b and H_c lie on the circle with diameter BC. The perpendicular bisector of the segment H_bH_c passes through the center M of this circle. This suggests the following construction:

Find the point M at the intersection of aa and the perpendicular bisector of H_bH_c. Draw a circle centered at M through either H_b or H_c. Extend BH_c and CH_b until they intersect at A.

Second Construction (Barukh Ziv)

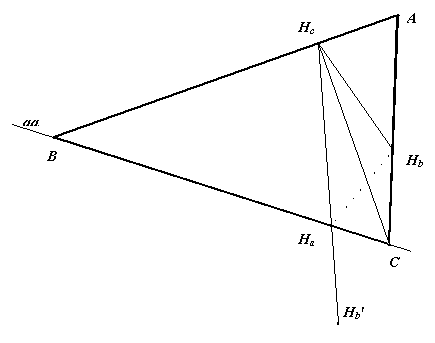
Recalling the mirror property of the orthic triangle, we conclude that angles BH_aH_b and CH_aH_b are equal. This suggests the following construction. Join points H_b, H_c. Reflect H_b in aa, call the image H_b'. Then intersection of H_cH_b' with aa is point H_a. Bisector of the angle H_bH_cH_a intersects aa at point C. Through point H_c draw a perpendicular to H_cC, which intersects aa at B. Finally, the intersection of BH_c with CH_b is point A.
a, h_b, l_c
Draw an auxiliary triangle BCH_b and the bisector of the angle C. On this bisector, select L_c so that CL_c = l_c. Extend BL_c and CH_b until they meet at A.
h_a, h_b, c
Draw an auxiliary triangle ABH_b and the circle with radius h_a centered at A. Draw a tangent from B to the circle. Extend the tangent and AH_b until they meet at C.

A second solution starts with a circle, say, ω on c as a diameter. One of the endpoints id naturally A, the other B. Draw circles C(A, h__a) and C(B, h__b) and find their intersections with ω. These will be the feet of the altitudes H_a and H_b from A and B, respectively. C lies at the intersection of BH_a and AH_b.
a, b, h_a

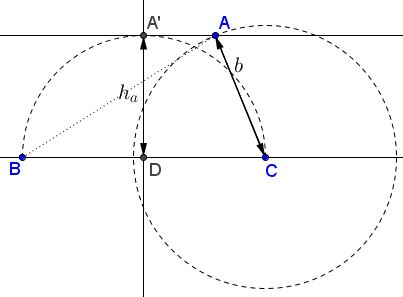
Let BC = a. Draw a line parallel to BC at distance h_a. Sweep an arc with center C and radius b. This will intersect the line in the sought vertex A.
h_a, h_b, m_c
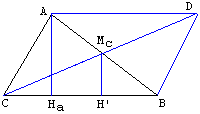
Assume the triangle ABC has been constructed. From M_c drop a line M_cH' perpendicular to CB. Then M_cH' is half h_a. This suggests the following construction:

First construct the right triangle CM_cH' with M_cH' = h_a/2 and hypotenuse CM_c = m_c. CH' defines the line aa. Similarly, on the other side of CM_c find the line bb. Extend CM_c to twice its length to get the point D from which draw lines parallel to aa and bb to obtain A and B, respectively.

71535616