Two Cevians and Proportions in a Triangle, I

Here is a problem #37 from the 1965 Annual High School Contest

Point D is selected on side AB of triangle ABC in such a way that AD:BD = 1:3 and point E is selected on side BC so that CE:BE = 1:2. The point of intersection of AE and CD is F. Then

DF/CF + AF/EF is

(A) 4/5 (B) 5/4 (C) 3/2 (D) 2 (E) 5/2

Solution

Point D is selected on side AB of triangle ABC in such a way that AD:BD = 1:3 and point E is selected on side BC so that CE:BE = 1:2. The point of intersection of AE and CD is F. Then

DF/CF + AF/EF is

(A) 4/5 (B) 5/4 (C) 3/2 (D) 2 (E) 5/2

Solution

Draw EGH||AB:

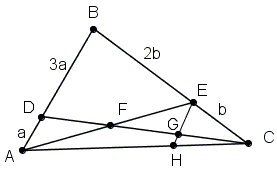
Then EG:3a = b:3b; EG = a = AD. Thus, DF = FG and AF = EF, so that AF/EF = 1.

Also, EH:4a = b:3b, EH = 4a/3 and GH = EH - EG = a/3. Hence, CG = CD/3 and DG = 2CD/3, and, since DF = FG, CF = 2CD/3.

It follows that DF/CF = 1/2 and, therefore, DF/CF + AF/EF = 1/2 + 1 = 3/2.

(Another solution is available eslewhere.)

References

C. T. Salkind, The Contest Problem Book II, MAA, 1996

41173631