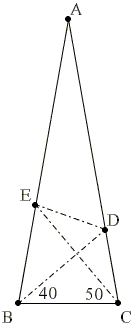
The 80-80-20 Triangle Problem, 40-50 Variant, Solution #1   Let ABC be an isosceles triangle (AB = AC) with BAC = 20°. Point D is on side AC such that CBD = 40°. Point E is on side AB such that BCE = 50°. Find the measure of CED. Solution Copyright © 1996-2008 Alexander Bogomolny                           This is one modification of the original problem that admits a practically trivial solution. Since BEC = 180° - 80° - 50° = 50°, ΔBCE is isosceles. In addition, DBE = 80° - 40° = 40° implying that BD is the angle bisector of the apex angle of an isosceles triangle. It is then also the median and the altitude from B. Thus BD divides CE in two and is perpendicular to it. Applying this information to ΔCDE we see that DB is the the altitude and also the median from D meaning that ΔCDE is isosceles: CD = DE and, more importantly,   CED = DCE = 80° - 50° = 30°. Copyright © 1996-2008 Alexander Bogomolny

28760749

Search:

All Products Apparel Baby Beauty Books DVD Electronics Home & Garden Gourmet Food Personal Care Jewelry & Watches Housewares Magazines Musical Instruments Music Computers Camera & Photo Software Sports & Outdoors Tools & Hardware Toys & Games VHS Computer Games Cell Phones

Keywords:

Latest on CTK Exchange Math Posted by Laura 2 messages 06:56 AM, Apr-15-08 Divisibility rules - Jargon buste ... Posted by Carolyn 2 messages 08:35 AM, Apr-04-08 drawing puzzle Posted by martin gran 31 messages 06:53 PM, May-09-08 conway's game of life Posted by frequency 0 messages 11:52 PM, May-12-08 Mistake on the page (an aside, Be ... Posted by Max 4 messages 10:28 AM, Feb-28-08 A Riddle Posted by idavis1 33 messages 06:59 AM, May-15-08 Josephus Flavius (correction) Posted by David Turner 1 messages 09:42 AM, May-14-08