Why Diameter Is the Longest Chord?
Indeed why? Why a diameter is the longest chord in a circle? I sometimes heard and several times read at popular math sites that the reason why a diameter is the longest chord is that a diameter passes through the center of the circle. While that is true that passing through the center has something to do with the length of a chord, the answer, as given, is vacuous. Since the definition of a diameter is a chord passing through the center of the circle, such an explanation actually reads: "The diameter is the longest chord in a circle because it is a diameter of the circle." How much does that explain?
Let's recollect the definitions:
A segment of a straight line joining two points on a circle is called a chord; a chord that passes through the center of the circle is called a diameter. (Ambiguously, the word "diameter" also denotes the length of a diameter.)
As the statement is definitely not an axiom of geometry, it must be proved, i.e., logically derived from simpler statements and the definitions.
Incidentally, Euclid proved that statement in the third book of his Elements as a more informative Proposition XV:
Of straight lines in a circle the diameter is greatest, and of the rest the nearer to the center is always greater than the more remote.
On a casual inspection, it seems obvious:

Nonetheless, it has to be proved and Euclid proves the first part with the reference to the Triangle Inequality (I.20) and the second part to the Pythagorean theorem.
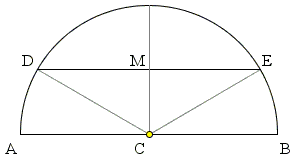
Let $AB$ be a diameter of the circle with center $C$ and $DE$ a chord not through $C.$ Then, by the definition of the circle as the locus of points equidistant from the center, $CA = CB = CD = CE = R,$ the radius of the circle. Which makes $AB = 2R.$ (The diameter is twice as long as the radius.)
On the other hand, in $\Delta CDE,$ by the triangle inequality,
$DE\lt CD + CE = R + R= 2R = AB.$
The same route is taken in my favorite Kiselev's Geometry. In another geometric classics, Lessons in Geometry by J. Hadamard the triangle inequality is applied differently, after establishing the fact that, for a point $P$ on the diameter $AB,$ one of the ends of the diameter is farthest from P among all points of the circle and the other is nearest.
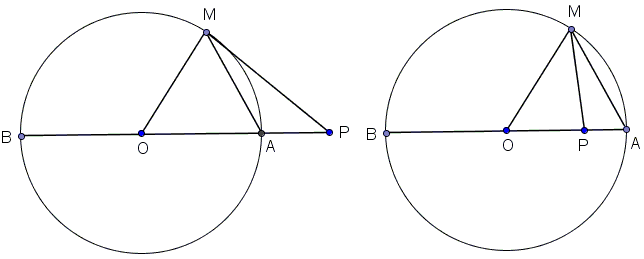
Pick point $P$ not on a circle, pass a line through $P$ and the center of the circle. The line will meet the circle in two points $A$ and $B.$ Let $A$ be the nearest of the two to $P.$ Then $AP$ is the (absolute) difference between $OP$ and $OA = R,$ $BP$ is the sum of $OP$ and $R.$ Let $M$ be any other point on the circle. In $\Delta OMP,$
$PM \gt |OP - OM| = |OP - R| = |OP - OA| = AP.$
Also,
$PM \lt OP + OM = OP + R = BP.$
Thus, of all points on the circle, $A$ is the nearest while $B$ is the farthest from $P.$ Observe now that the two inequalities that express this fact are valid also for $P$ on the circle. Let $P$ coincide with $A.$ Then, for any $M \ne B,$ $MA \lt AB$, meaning that the diameter $AB$ is longer than the chord $MA.$
A third proof makes use of the Pythagorean and Thales' theorems. If $AB$ is a diameter and $M$ a point on a circle different from $A$ and $B,$ then $\Delta AMB$ is right at $M.$ The Pythagorean theorem tells us that $AM^{2} + BM^{2} = AB^{2},$ implying in particular that, say, $AM \lt AB.$
Note: Vincent Pantaloni observed that conversely,
The longest chord in a circle passes through the center of the circle and is, therefore, a diameter.
Indeed, let $AB$ be the longest chord in circle $(O)$ centered at $O.$ Let $AO$ meet the circle the second time in $B'.$ Then
$AB' = 2R = OA + OB \ge AB,$
implying (since $AB$ was said to be the longest chord) $AB' = AB,$ so that $B = B'$ and $O$ lies on $AB.$
There is another proof exploiting the (all-around) symmetrical nature of the circle.
Let $AB$ be a chord of circle $(O)$ that is not a diameter. Reflect the circle in $AB.$ Note that any axis of symmetry of a circle ought to pass through its center (because a perpendicular bisector of a chord always goes through the center of the circle.) Since $AB$ is not a diameter, it could not be an axis of symmetry either, thus the reflection gives us another circle $(O')$ in which $AB$ is also a chord. Moreover, $AB\perp OO'.$
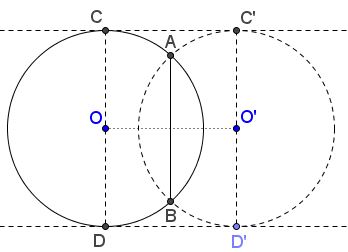
Let $CC'$ and $DD'$ be the common tangents of the two circles. In particular, $OC\perp CC'\perp O'C'$ and similarly for the second tangent. $AB$ does not cross $CC'$ for, if it did, $OA$ would be longer than $OC,$ which could not be. So, there is a rectangle $CDD'C'$ and, within, line segment $AB$ parallel to, say, $CD,$ implying $AB\lt CD.$
References
- A. Givental, Kiselev's Geometry. Book I. PLANIMETRY, Sumizdat, 2006, p. 88.
- J. Hadamard, Lessons in Geometry , Education Development Center, Dec 2006, Corollary to Theorem 64.
- R. Simson, The Elements of Euclid, Eliborn Classics, 2005, p. 65
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71537242
