Mechanical Proofs of the Pythagorean Theorem

The Pythagorean theorem is arguably one of the most fundamental results in mathematics, with more known proofs than probably any other theorem. It is satisfying to know that the theorem lurks in many mechanical phenomena as demonstrated below. There is clearly more than one sense in which it deserves the designation of fundamental.

Imagine a right triangular prism with a right triangle as a base [Mark Levi, p. 10]. Let the legs of the triangle be a, b, and the hypotenuse c. Imagine the prism filled with water and mounted on a vertical spindle at one of the acute angles of the base triangle. The prism can freely rotate around the spindle. Will it?

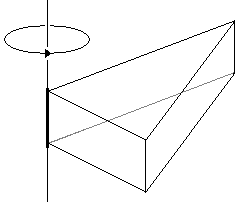
The answer is naturally, No. A prism left to its own advices will not move any way and stay at rest. This means that the forces acting on the prism somehow balance out. Beside the vertical gravitational pull that is balanced by the spindle's resistance, what are other forces that act on the prism?

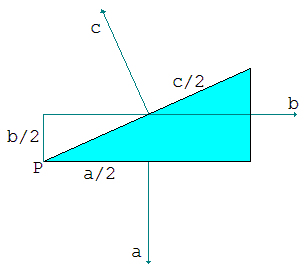
The water pushes from inside on each of the side faces of the prism. The push is proportional to the area of the side and, since all of them are rectangles of the same height, to their lengths. This force at each side generates a torque (momentum) as if it was concentrated at the center of gravity - the center - of the side. The torques on the legs pull the prism in one direction, the torque on the hypotenuse in the other. The torques balance. Each is the product of the distance to the axis times the force applied. As the result,

a² + b² = c².

Consider now material point C that can slide without friction over a rigid semicircle with a diameter AB and center at O [Mark Levi, pp. 21-23]. Imagine two identical springs that link C to the points A and B and assume that the springs satisfy Hooke's law: F = κx, where x is the elongation of the spring, κ Hooke's constant, and F the tension of the spring, i.e. the force it exerts at both end points. The average force needed to stretch the spring to length x is κx/2 and the work performed is then the product of the distance and the force: W(x) = κx²/2. This is also the potential energy of the spring stretched to length x.

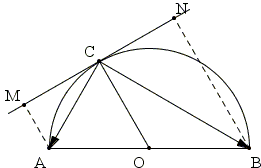
Returning to our configuration, we claim that point C is in equilibrium at any position on the semicircle. Indeed, since the radial forces can't cause it to move along the circle, suffice it to prove that the tangential components of the tension exerted by the two springs balance out.

Let M and N be the projections of A and B onto the tangent to circle at C. The lengths of CM and CN are proportional to the projections of the two forces on the tangent. But CM = CN because these are caught between three parallels AM, CO, and BN (remember that CO ⊥ MN also), while AO = BO by construction.

As a consequence, the potential energy of the two springs is the same for any position of C. In particular, for a position with AC = b and BC = a, P(x) = κ(a² + b²)/2. For the position at one of the end points, P(0) = κ(0² + c²)/2, where c is the diameter of the semicircle: c = AB. It follows that a² + b² = c².

If a puck of mass m = 1 is pushed on frictionless ice so as to acquire velocity a, its kinetic energy will be a²/2 [Mark Levi, p. 25]. If its pushed in the perpendicular direction and acquire velocity b, its kinetic energy will be b²/2. Consecutively executed pushes, on the one hand, will supply the puck with kinetic energy a²/2 + b²/2. On the other hand, the puck will acquire velocity c which is geometrically the diagonal of the rectangle with sides a and b. Its kinetic energy is c²/2 and we are done.

References

1. M. Levi, The Mathematical Mechanic, Princeton University Press, 2009

Copyright © 1996-2010 Alexander Bogomolny