A Number Theoretic Problem With the Floor Function

$\displaystyle\bigg\lfloor\frac{n}{1}\bigg\rfloor +\bigg\lfloor\frac{n}{2}\bigg\rfloor +\bigg\lfloor\frac{n}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{n}{n}\bigg\rfloor = t_{1}+t_{2}+\ldots +t_{n},$

where $t_{a}$ is the number of divisors of integer $a.$

The proof is by induction. For $n=1$ the identity is obviously true. Assume it is true for $n=k:$

$\displaystyle\bigg\lfloor\frac{k}{1}\bigg\rfloor +\bigg\lfloor\frac{k}{2}\bigg\rfloor +\bigg\lfloor\frac{k}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{k}{k}\bigg\rfloor = t_{1}+t_{2}+\ldots +t_{k},$

and let prove it for $n=k+1.$ For an integer $m,$ $0\gt m\le n+1,$ we need to consider two cases:

1. $m$ divides $n+1$

   $n+1 = ms,$ making $\displaystyle\bigg\lfloor\frac{n+1}{m}\bigg\rfloor =\frac{n+1}{m}=s$ whereas clearly $\displaystyle\bigg\lfloor\frac{n}{m}\bigg\rfloor =\frac{n}{m}=s-1,$ implying $\displaystyle\bigg\lfloor\frac{n+1}{m}\bigg\rfloor =\bigg\lfloor\frac{n}{m}\bigg\rfloor +1.$

2. $m$ does not divide $n+1$

   $n+1 = ms+r,$ $1\le r\lt n+1.$ Then $n = ms+(r-1),$ $1\le r\lt n+1.$ Therefore,

   $\displaystyle\bigg\lfloor\frac{n+1}{m}\bigg\rfloor =s=\bigg\lfloor\frac{n}{m}\bigg\rfloor.$

   In conclusion,

   $\begin{cases} \displaystyle\bigg\lfloor\frac{n+1}{m}\bigg\rfloor =\bigg\lfloor\frac{n}{m}\bigg\rfloor + 1 & \mbox{if } m \mbox{ divides } n+1 ,\\ \displaystyle\bigg\lfloor\frac{n+1}{m}\bigg\rfloor =\bigg\lfloor\frac{n}{m}\bigg\rfloor & \mbox{if } m \mbox{ does not divide } n+1 . \end{cases}$

   It follows that

   $ \begin{align} \displaystyle\bigg\lfloor\frac{k+1}{1}\bigg\rfloor &+\bigg\lfloor\frac{k+1}{2}\bigg\rfloor +\bigg\lfloor\frac{k+1}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{k+1}{k+1}\bigg\rfloor\\ &= \bigg\lfloor\frac{k}{1}\bigg\rfloor +\bigg\lfloor\frac{k}{2}\bigg\rfloor +\bigg\lfloor\frac{k}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{k}{k}\bigg\rfloor +t_{k+1}, \end{align}$

   which proves the statement.

The number of terms in the sequence $1,2,3,\ldots,n$ divisible by a number $m$ equals $\displaystyle\bigg\lfloor\frac{n}{m}\bigg\rfloor.$ These are the numbers $m,2m,3m,\ldots$ Thus the expression

$\displaystyle\bigg\lfloor\frac{n}{1}\bigg\rfloor +\bigg\lfloor\frac{n}{2}\bigg\rfloor +\bigg\lfloor\frac{n}{3}\bigg\rfloor +\ldots +\bigg\lfloor\frac{n}{n}\bigg\rfloor$

sums up the total number of the integers not exceeding $n$ divisible by $1$ plus the number of those that are divisible by $2,$ and so on, effectively adding up the number of all the divisors of the members of the sequence $1,2,\ldots ,n$ i.e., $t_{1}+t_{2}+\ldots +t_{n}.$

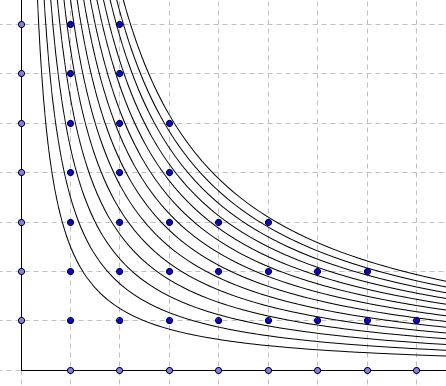
This proof is actually a geometric illustration for Solution #2.

Consider all the hyperbolas $y=k/x$ with integer $k\le n.$ The fact that point $(p,q)$ lies on the hyperbola $y=k/x$ means exactly that both $p$ and $q$ are among the divisors of $k.$ Thus the number of divisors of $k$ is the number of integer grid points on the graph of the hyperbola $y=k/x.$ Therefore the total number of the divisors of positive integers not exceeding $n$ is the number of grid points below and on the hyperbola $y=n/x.$

On the other hand, for a given $p,$ the number of points in the column $x=p$ below or on the hyperbola $y=n/x$ equals $\displaystyle\bigg\lfloor\frac{n}{p}\bigg\rfloor.$ Thus the statement at hand simply shows that the two ways of counting grid points is indeed the same.

1. D. O. Shklarsky, N. N. Chentzov, I. M. Yaglom, The USSR Olympiad Problem Book: Selected Problems and Theorems of Elementary Mathematics, Dover Publications; 3 Revised edition (September 28, 1993), Problem 103(a)