An Identity in (Cyclic) Quadrilaterals
Problem
Let $ABCD$ be a cyclic quadrilateral; $E$ the intersection of the diagonals.
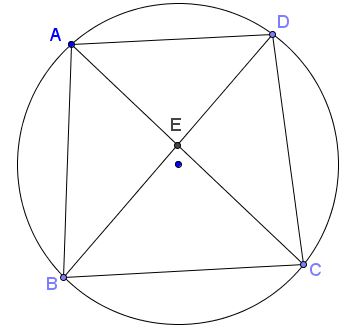
Then
$\displaystyle\frac{AE}{CE}=\frac{AB}{BC}\cdot\frac{AD}{CD}.$
Solution
Introduce the angles as shown in the diagram below$
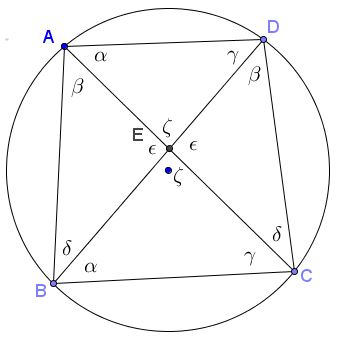
I shall apply the Law of Sines repeatedly in several triangles:
$\begin{align}\displaystyle \Delta ABE: & \frac{AE}{BE}=\frac{\sin\delta}{\sin\beta},\\ \Delta BCE: & \frac{BE}{CE}=\frac{\sin\gamma}{\sin\alpha},\\ \Delta ABC: & \frac{AB}{BC}=\frac{\sin\gamma}{\sin\beta},\\ \Delta ACD: & \frac{AD}{CD}=\frac{\sin\delta}{\sin\alpha}. \end{align}$
Multiplying the first and the second pair separately yields:
$\displaystyle \frac{AE}{CE}=\frac{AE}{BE}\frac{BE}{CE}=\frac{\sin\delta}{\sin\beta}\frac{\sin\gamma}{\sin\alpha}=\frac{AB}{BC}\frac{AD}{CD},$
which proves the statement.
Observation
The identity $\displaystyle\frac{AE}{CE}=\frac{AB}{BC}\cdot\frac{AD}{CD}$ is a necessary but not a sufficient condition for the quadrilateral $ABCD$ to be cyclic. The clue why this be so stems from its lack of symmetry. It compares poorly with the symmetry exhibited by Ptolemy's theorem that naturally comes to mind.
It is easy to exploit this lack of symmetry. Start with a square which is naturally cyclic:
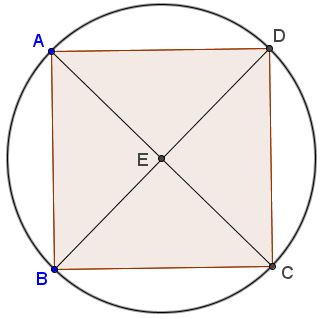
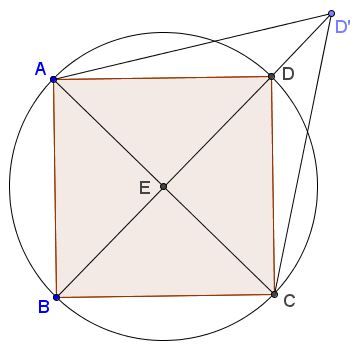
Now, extend vertex $D$ along the diagonal $BD$ to a new position $D'.$ We still have $\displaystyle\frac{AE}{CE}=\frac{AB}{BC}\cdot\frac{AD'}{CD'}$ (because $\displaystyle\frac{AD}{CD}=1=\frac{AD'}{CD'})$ but the quadrilateral $ABCD'$ is no longer cyclic.
Acknowledgment
The problem has been posted by Dao Thanh Oai (Vietnam) at the CutTheKnotMath facebook page.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73561702
