The Final Chapter of the Asymmetric Propeller Story
What is this about?
Problem
Given three similar triangles $A_{1}B_{1}C_{1},$ $A_{2}B_{2}C_{2},$ $A_{3}B_{3}C_{3}.$ The centroids of the triangles $A_{1}A_{2}A_{3},$ $B_{1}B_{2}B_{3},$ and $C_{1}C_{2}C_{3}$ form a fourth similar triangle
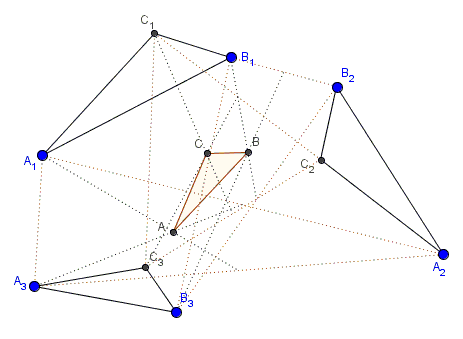
Hint
I am afraid this is going to be either vectors or complex numbers. Hopefully, using spiral similarities will simplify the proof.
Solution
Let $S$ and $T$ be spiral similarities that map $A_{1}B_{1}C_{1}$ onto $A_{2}B_{2}C_{2}$ and $A_{3}B_{3}C_{3},$ respectively:
$S(A_{1}B_{1}C_{1})=A_{2}B_{2}C_{2}$ and
$T(A_{1}B_{1}C_{1})=A_{3}B_{3}C_{3}.$
Define $A=(A_{1}+A_{2}+A_{3})/3 = (A_{1}+S(A_{1})+T(A_{1}))/3.$ The affine operator $M = (I+S+T)/3,$ where $I$ is the identity operator, preserves angles such that if $B=M(B_{1})$ and $C=M(C_{1})$ triangle $ABC$ is similar to $\Delta A_{1}B_{1}C_{1}.$
That's all folks.
Acknowledgment
The problem of the Asymmetric Propeller has a long history. The original problem underwent several generalizations associated with the names of Martin Gardner, Leon Bankoff, Paul Erdös, Murrey Klamkin, and Ross Honsberger. The problem relates to the Fundamental Theorem of 3-Bar Motion discovered by William Kingdom Clifford and Arthur Cayley.
Most recently, Dao Thanh Oai has posted at the CutTheKnotMath facebook page a special case of the above statement where the three given triangles were equilateral. The post brought up the memory of the Asymmetric Propeller which led to the more general case of three similar triangles, as stated above. In all likelihood, this is the most natural environment for the problem.
Asymmetric Propeller
- Asymmetric Propeller (An Interactive Gizmo)
- Asymmetric Propeller: a Generalization
- A Case of Similarity
- Napoleon's Propeller
- Asymmetric Propeller and Napoleon's Theorem
- Asymmetric Propeller by Plane Tiling
- The Final Chapter of the Asymmetric Propeller Story
- Asymmetric Propeller, the XXI Century
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71753262
