There exist triangular numbers that are also square

This fact was no longer news to me when in September 2000 I received a message from Armando Guarnaschelli, Argentina. A Microsoft Word file has been attached to the message with a penetrating observation into the problem. Unfortunately, I could not convert the Word file into HTML - the language of the Web, whereas retyping it into HTML in its entirety seemed to be too arduous a job. With my apologies to Armando, I here present his results in my own words.

Closely studying the table of the numbers that are both triangular and square, Armando made an interesting observation. Let x be the side of the triangular T(x), y the side of the square Q(y). The numbers in the same row of the table have the property that T(x) = Q(y). Let x₁ and y₁ be two such numbers. Then there exists two other numbers x₂ and y₂ in the table such that

x1 + y1 = x2 - y2.

In fact, the second pair of the numbers lies in the row immediately following that of the first pair.

Let's prove that this is always the case. In other words, let's assume that T(x₁) = Q(y₁). Then there exist x₂ and y₂ such that

x1 + y1 = x2 - y2, and T(x2) = Q(y2).

Introduce u = x₁ + y₁ and assume that x₂ and y₂ do exists. Let's see where this assumption may lead us. (Note that the deductive steps will be reversible.) Then y₂ = x₂ - u, and T(x₂) = Q(y₂) yield a quadratic equation

x22 - x2(4u + 1) + 2u2 = 0,

from which x₂ is expressed as

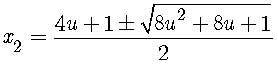
Having in mind that T(x₁) = Q(y₁), one can show that 8u² + 8u + 1 = (2x₁ + 4y₁ + 1)², which leads to a more straightforward expression for x₂:

x2 = ((4x1 + 4y1 + 1) ± (2x1 + 4y1 + 1))/2.

The minus sign leads to x₂ = x₁, from which y₂ would be equal to -y₁ < 0. Thus we are left with the only meaningful

x2 = ((4x1 + 4y1 + 1) + (2x1 + 4y1 + 1))/2 = 3x1 + 4y1 + 1

From y₂ = x₂ + u we easily find y₂. I'll write the two expressions together:

(*)	x2 = 3x1 + 4y1 + 1 y2 = 2x1 + 3y1 + 1

This is how simple it finally becomes. Starting with one pair (x, y) such that T(x) = Q(y), we can use the recurrence (*) to obtain infinitely many such pairs. Let's for example start with the first row: (x, y) = (1, 1). (*) gives successively (8, 6), (49, 35), (288, 204), etc. - row after row. It appears that the recurrence (*) generates the whole table of all possible pairs (x, y).

This is indeed so. To see why, solve (*) for x₁ and y₁:

(**)	x1 = 3x2 - 4y2 + 1 y1 = -2x2 + 3y2 - 1

(*) yields increasing sequences of x and y. (**) yields decreasing sequences. However, using T(x) = Q(y) it can be shown

that if x > 1 and y > 1, then 3x - 4y + 1 > 0 and also -2x + 3y - 1 > 0.

Assume on the contrary that x and y with T(x) = Q(y) have not been obtained from (*) starting with (1, 1). From (**) we get decreasing sequences of x and y none of which belongs to the table but all are positive. Since neither of the sequences may be infinite the pair (1, 1) is bound to appear sooner or later. Contradiction.

I remove my hat to Armando Guarnaschelli.

|Contact| |Front page| |Contents| |Did you know?|

Copyright © 1996-2018 Alexander Bogomolny