Toying With The Geoboard

To better appreciate the power of Pick's theorem try answering a few questions below without invoking the theorem. The questions are posed for the geoboard.

Form a triangle with a base connecting two consecutive nodes on a horizontal line. Let the apex be two horizontal lines away. Whatever the position of the apex, the sides of the triangle will, between them, pass through one and only one additional grid point.
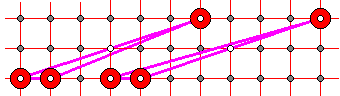
A similar question for triangles with altitude equal 3. Depending on the position of the apex either two grid nodes lie on one side or one lies in the interior of the triangle.
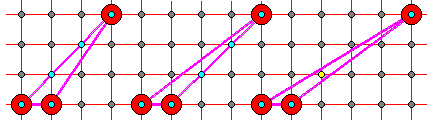
When the base of the triangle is of length 2 or more, triangles acquire enterior nodes. As the apex moves, boundary and enterior nodes appear in certain (periodic) combinations. It pasys to look for invariants.
Which of the three simple polygons has the greatest area?
Here's one interesting question unrelated to Pick's theorem. As the diagrams above show, it is possible to position vertices of a simple polygon at the nodes forming a 4x4 array. Note that, as implemented, unless you exercise caution it is not always simple to position the vertices at the desired nodes. If you have enough space to drag the vertices, the task becomes easier. A natural restriction comes about when you try to use all available nodes (there's 9x12 of them.)

Pick's Theorem
- Exercises for the Geoboard
- Pick's Theorem, A Proof
- Farey Series
- Pick's Theorem Applies to the Farey Series
- Stern-Brocot Tree
- Applications of Pick's Theorem

40614695