Quadratic Formula
Completing And Not Completing the Square
Introduction
| The importance of the investigations connected with the expression $ax^{2} + bx + c,$ can hardly be overrated, at least to those students who pursue mathematics to any extent. In the higher branches, great familiarity with these results is indispensible. |
| A. De Morgan (1806-1871) |
| On the Study and Difficulties of Mathematics |
| Dover, 2005, p. 149 |
By the Fundamental Theorem of Algebra, every polynomial $P_{n}(x)$ of degree $n$ with complex coefficients has $n$ (perhaps repeated) complex roots. Here we are concerned with the case of $n = 2$ and the polynomials of second degree. Such polynomials are in the form
$P(x)=ax^{2} + bx + c,$
where $a$ is assumed not to be zero: $a\ne 0.$ A quadratic polynomial is assured to have two roots, say, $x_{1}$ and $x_{2},$ such that it admits a factorization
$P(x)=ax^{2} + bx + c =a(x- x_{1})(x- x_{2}).$
The two roots can be found by means of what is known as a Quadratic Formula:
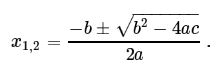
Below we offer several derivations of that formula.
Example
Solve $2x^{2} - 7x + 3 = 0,$ with $a = 2,$ $b = -7,$ $c = 3.$ The quadratic formula gives:
$\begin{align} x &= (7 \pm \sqrt{(-7)^{2} - 4\cdot 2\cdot 3}) / 2\cdot 2\\ &= (7 \pm \sqrt{49 - 24}) / 4\\ &= (7 \pm \sqrt{25}) / 4\\ &= (7 \pm 5) / 4\\ \end{align}$
producing two roots, say, $x_{1} = (7 + 5) / 4 = 3$ and $x_{2} = (7 - 5) / 4 = 1/2.\;$ It can be also verified that
$2x^{2} - 7x + 3 = 2(x - 3)(x - 1/2).$
First Derivation
The formula is often derived by the process of completing a square, based on a well known (and easily verifiable) algebraic identity
$(u+ v)^{2} =u^{2} + 2uv+ v^{2}.$
So, for example, if we can identify an expression as $u^{2} + 2uv,$ then to complete the squarewe need to add to it $v^{2}$ which converts the sum of two terms $u^{2} + 2uv$ into a single square $(u + v)^{2}.$
We start with the quadratic equation $ax^{2} + bx + c = 0$ and move the free termto the right:
$ax^{2} + bx = -c.$
The left hand side can be seen to be an incomplete square in the form $u^{2} + 2uv$. Indeed,
$\begin{align} ax^{2} + bx &= (\sqrt{a} x)^{2} + 2(\sqrt{a} x)(b / 2\sqrt{a}) \\ &= (\sqrt{a} x)^{2} + 2(\sqrt{a} x)(b / 2\sqrt{a}) + (b / 2\sqrt{a})^{2} - (b / 2\sqrt{a})^{2}. \end{align}$
(Here $u= \sqrt{a} x$ and $v=b/ 2\sqrt{a}$). We can continue to transform the quadratic equation step by step:
$ax^{2} + bx + c = 0,$
$ax^{2} + bx = -c,$
$(\sqrt{a} x)^{2} + 2(\sqrt{a} x)(b / 2\sqrt{a}) + (b / 2\sqrt{a})^{2} = - c + (b / 2\sqrt{a})^{2},$
$(\sqrt{a} x + b / 2\sqrt{a})^{2} = - c + (b / 2\sqrt{a})^{2},$
$(2ax + b)^{2} = - 4ac+ b^{2},$
$2ax + b = \pm \sqrt{b^{2} - 4ac},$
$2ax = \pm \sqrt{b^{2} - 4ac} - b,$
$x = (-b \pm \sqrt{b^{2} - 4ac}) / 2a.$
Note that the derivation may be simplified somewhat typographically by first converting the equation to $\displaystyle x^2+\frac{b}{a}x+\frac{c}{a}=0.$
Second Derivation
There is a much simpler way to derive the quadratic formula. Multiply the equation $ax^{2} + bx + c = 0$ by $4a$ to obtain $4a^{2}x^{2} + 4abx + 4ac= 0.$ But then
$\begin{align} 4a^{2}x^{2} + 4abx + 4ac &= (2ax)^{2} + 2\cdot (2ax)(b) + 4ac\\ &= (2ax + b)^{2} - b^{2} + 4ac.\\ \end{align}$
In other words, $(2ax + b)^{2} =b^{2} - 4ac.$ Taking the square root,
$2ax + b = \pm \sqrt{b^{2} - 4ac}.$
Rearranging the terms and dividing by $2$ adirectly leads to the quadratic formula.
Third Derivation
I am grateful to Michael Brozinsky for bringing this derivation to my attention.
The factorization $a(x-x_{1})(x-x_{2})$ of a quadratic polynomial $ax^2+bx+c,$ with two roots $x_1$ and $x_2,$ leads Viète's formulas: $a(x_1+x_2)=-b$ and $a(x_1\cdot x_2)=c.$ A change of variables, say, $\displaystyle z=x+\frac{b}{2a},$ yields two numbers $\displaystyle z_{1}=x_{1}+\frac{b}{2a}$ and $\displaystyle z_{2}=x_{2}+\frac{b}{2a},$ that add up to $0:$ $z_1+z_2=0,$ implying they are the roots of a quadratic equation $z^2 + z_1\cdot z_2=0.$ So we have
$\begin{align}\displaystyle 0 &= z^2 + z_1\cdot z_2 \\ &= z^2 + (x_{1}+\frac{b}{2a})(x_{2}+\frac{b}{2a}) \\ &= z^2 + x_{1}x_{2} + (x_{1}+x_{2})\frac{b}{2a} + \frac{b^2}{4a^2} \\ &= z^2 + \frac{c}{a} - \frac{b}{a}\frac{b}{2a} + \frac{b^2}{4a^2} \\ &= z^2 + \frac{4ac - 2b^2 + b^2}{4a^2} \\ &= z^2 + \frac{4ac - b^2}{4a^2}. \end{align}$
In other words, $\displaystyle z^2 = \frac{b^2 - 4ac}{4a^2}$ and, as a consequence, $\displaystyle z_{1,2} = \frac{\pm\sqrt{b^2 - 4ac}}{2a}$ and, finally, with the back substitution,
$\displaystyle x_{1,2} = \frac{\pm\sqrt{b^2 - 4ac}}{2a}-\frac{b}{2a}=\frac{-b\pm\sqrt{b^2 - 4ac}}{2a}.$
Fourth Derivation
Let it be required to solve the equation $ax^2+bx+c=0.\;$ We proceed in several steps:
$\begin{align} &ax^2+c=-bx,\\ &(ax^2+c)^2=(-bx)^2,\\ &a^2x^4+2acx^2+c^2=b^2x^2,\\ &(a^2x^4+2acx^2+c^2)-4acx^2=b^2x^2)-4acx^2,\\ &a^2x^4-2acx^2+c^2=(b^2-4ac)x^2,\\ &(ax^2-c)^2=(b^2-4ac)x^2,\\ &ax^2-c=\pm\sqrt{b^2-4ac}x. \end{align}$
Adding to this $ax^2+c=-bx\;$ we get $2a^2x^2=(-b\pm\sqrt{b^2-4ac})x\;$ such that $\displaystyle x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.$
References
- H. Heaton, A Method of Solving Quadratic Equations, The American Mathematical Monthly, Vol. 3, No. 10 (Oct., 1896), pp. 236-237
Fifth Derivation
The strating point is the equation $x^2+x=a$ where the left-hand side is the product of two factors that differe by $1.\;$ The two factors $\displaystyle\left(a+\frac{1}{2}\right)\left(a-\frac{1}{2}\right)=a^2-\frac{1}{4}\;$ give such an example and can be amended to satisfy the entire requirement:
$\displaystyle\left(\sqrt{a+\frac{1}{4}}+\frac{1}{2}\right)\left(\sqrt{a+\frac{1}{4}}-\frac{1}{2}\right)=a.$
Here the smaller of the two factors, viz., $\displaystyle x=\sqrt{a+\frac{1}{4}}-\frac{1}{2}\;$ is the root of $x^2+x=a.$
The more general equation - $x^2+bx=a\;$ - is solved similarly:
$\displaystyle\begin{align} &x(x+b)=a,\\ &\sqrt{a}(\sqrt{a}+b)\ne a,\\ &\left(\sqrt{a}+\frac{b}{2}\right)\left(\sqrt{a}-\frac{b}{2}\right)=a-\frac{b^2}{4},\\ &\left(\sqrt{a+\frac{b^2}{4}}+\frac{b}{2}\right)\left(\sqrt{a+\frac{b^2}{4}}-\frac{b}{2}\right)=a,\\ &x=\sqrt{a+\frac{b^2}{4}}-\frac{b}{2}. \end{align}$
Getting the larger root is left to the reader.
References
- J. W. Cirul, A Method of Solving Quadratic Equations, The American Mathematical Monthly, Vol. 44, No. 7 (Aug. - Sep., 1937), pp. 462-463
Sixth Derivation
This derivation has been suggested by Uzair Baig. It is simple but not elementary in the sense that it assumes knowledge of derivatives.
Let $f(x)=a x^2 + b x +c.\;$ Then $f'(x^*) =0\;$ where $\displaystyle x^*= -\frac{b}{2a}.\;$ Define $g(x)=f(x+x^*),\;$ i.e., $\displaystyle g(x)= ax^2 + \left(c- \frac{b^2}{4 a}\right).\;$ Now, $g(x)=0\;$ is easily solved, giving two roots, $\displaystyle x_{1,2}= \pm\frac{\sqrt{b^2-4ac}}{2a}.\;$ This tells us that $f(x)=0\;$ for $\displaystyle x_{1,2}= \pm\frac{\sqrt{b^2-4ac}}{2a}-\frac{b}{2a}\;$ which is the quadratic formula.
Discriminant
Obviously, the expression $D=b^{2} - 4ac$ that appears in the quadratic formula under the square root plays an important role in solving quadratic equations. Because of its importance it was given a name. $D=b^{2} - 4ac$ is called the discriminant of the quadratic equation $ax^{2} + bx + c = 0.$ As the quadratic formula shows, there are three possible cases:
- $D\gt 0.$ In this case, the equation has two distinct real roots.
- $D= 0.$ In this case, the two roots coalesce into one, which is called a double root implying that the are still two roots albeit equal.
- $D\lt 0.$ In this case, the equation has to complex roots which, for real a, b, c, are conjugate.
An Aside
For quadratic polynomials with real coefficients, the roots come in pairs as manifest by the "$\pm$" symbol. For the polynomials with real coefficients but complex roots, the roots in such pairs are conjugate. (An interactive illustration of the behavior of the roots as the function of the coefficients is available elsewhere.) We now know that the same holds for all polynomials with real coefficients of degree higher than $1.$ This means that any polynomial with real coefficients admits a decomposition into a product of linear and quadratic terms. However, this fact was not always known of course. In the 17th century, this was still a conjecture. The Fundamental Theorem of Algebra is the product of the 19th century. According to [W. Dunham, p. 109],
No less an authority than Leibniz doubted that every real polynomial can be factored into real linear and/or real quadratic pieces. Worse, Nicolaus Bernoulli (1687-1759) claimed to have found a counter example - namely, $x^{4} - 4x^{3} + 2x^{2} + 4x + 4$ - that could not be so factored. If he were correct, the game was over: the fundamental "theorem" of algebra would have been automatically disproved.
Euler, rising to the defence of this conjecture, showed that Bernoulli was wrong. In a 1742 letter to Christian Goldbach, he factored the supposedly unfactorable, splitting the quartic into the product of quadratics
$x^{2} - (2 + \sqrt{4 + 2\sqrt{7}})x + (1 + \sqrt{4 + 2\sqrt{7}} + \sqrt{7})$
and
$x^{2} - (2 - \sqrt{4 + 2\sqrt{7}})x + (1 - \sqrt{4 + 2\sqrt{7}} + \sqrt{7}).$
This factorization appears to lie somewhere between miraculous and preposterous. It looks ever so much like a misprint - but it is perfectly correct.
Every one is welcome to verity the correctness of Euler's feat.
References
- W. Dunham, Euler: The Master of Us All, MAA, 1999
Quadratic Formula and Equation
- Geometric Construction of Roots of Quadratic Equation
- Quadratic Formula - Completing And Not Completing the Square
- Graph and Roots of Quadratic Polynomial
- Emergence of Chaos
- Maximum Volume of a Cut Off Box
- Golden Ratio in Geometry
- Viète's Formulas
|Contact| |Front page| |Contents| |Algebra|
Copyright © 1996-2018 Alexander Bogomolny71752881
