Two 6s in a Row
Problem
Solution 1
Let $P(n)$ denote the probability that for the first time two successive $6s$ showed up on the tosses $n-1$ and $n.$ Obviously, $P(1)=0$ and $P(2)=p^2,$ with $\displaystyle p=\frac{1}{6}.$
Let $\mathbb{E}(n)$ be the expected number of tosses. There's no doubt that $\mathbb{E}(n)\gt 2.$ We denote the toss that came up with $6$ on top as $S,$ all other tosses are denoted collectively as $F.$ Any sequence of $S$ and $F$ starts with one of the four combinations: $SS,$ $SF,$ $FS,$ $FF.$ With the probability of $p^2$ of the first two successes we achieve the goal in just $2$ throws. In case of either $SF$ or $FF$ we have to add $2$ to the number of tosses and start counting again. $SF$ has the probability of $p(1-p);$ $FF$ the probability $(1-p)^2.$ Concerning the first two tosses being $FS$ which has the probability of $(1-p)p,$ the third toss may have two outcomes. If it's $S,$ we achieve our goal in $3$ tosses - this with the probability of $(1-p)p^2.$ If it's $F,$ we court three steps and continue as from the beginning. This happens with the probability of $(1-p)^2p.$ Thus we are led to the recurrence relation
$\begin{align} \mathbb{E}(n) &= 2\cdot p^2\\ &+(\mathbb{E}(n)+2)(p(1-p)+(1-p)^2)\\ &+3\cdot (1-p)p^2\\ &+(\mathbb{E}(n)+3)(1-p)^2p. \end{align}$
A few algebra steps yield
$\displaystyle \mathbb{E}(n)=\frac{2+p-p^2}{p^2(2-p)}=\frac{(2-p)(p+1)}{p^2(2-p)}=\frac{1}{p^2}+\frac{1}{p}.$
For $\displaystyle p=\frac{1}{6},$ $\displaystyle \mathbb{E}(n)=36+6=42.$
In passing, for a fair coin, $\displaystyle p=\frac{1}{2},$ so that $\mathbb{E}(n)=4+2=6.$
Solution 2
Expected throws $\mathbb{E}(t)$ until a $6$ is $6,$ so $\mathbb{E} = \mathbb{E}(t\mathbb{E}(t)+t) = \mathbb{E}(t)^2+\mathbb{E}(t) = 42.$
Solution 3
Using the Markov chain, we need three nodes: $S$ stands for any sequence of throws that does not end with a $6;$ $B$ is an intermediate node that denotes sequences that end with a single $6;$ $V$ is the finanal node for the sequences that end in two $6s.$
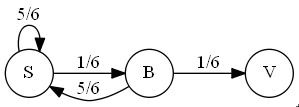
We derive two equations (borrowing the notations from the associated nodes. The equation
$\displaystyle V=1+\frac{1}{6}B+\frac{5}{6}V$
tells us that moving from a node via an attached arrow takes one throw of a die $(+1)$ in the diagram. Then with the probability of $1/6,$ i.e., of getting one $6,$ we move to a new state $B,$ while with the probability of $5/6$ we return to where we started (but still wasting one toss.)
The other equation is
$\displaystyle B=1+\frac{5}{6}V$
which tells us that with one toss we either get to the goal $V$, or back two the start $S.$
We can find $V$ from the two equations: $\displaystyle V=42,$ which conventionally counts the last throw.
Solution 4
Let us call $T(n),$ for $n\in\mathbb{N},$ a time at which $n$ successive $6s$ show up for the first time. For $n\in\mathbb{N},$ $T(n)$ is a random variable. We want to find $\mathbb{E}(T(2)).$ We know that $\mathbb{E}(T(1))=6.$ and that the game is a Markov process. For $n\gt 1,$ we have the following relation:
$\displaystyle \mathbb{E}(T(n+1))=\frac{1}{6}\left(\mathbb{E}(T(n))+1\right)+\frac{5}{6}\left(\mathbb{E}(T(n))+1+\mathbb{E}(T(n+1))\right).$
We then deduce that $\mathbb{E}(T(n+1))=6(\mathbb{E}(T(n))+1).$ Thus $\mathbb{E}(T(2))=42.$
Solution 5
Using Nielsen's result. $L-letter$ alphabet, with $L=6,$ target string $S$ of $n$ letters. Let $S'$ be longest common prefix and suffix of $S$ (excluding the case of $S'=S).$ Then $\mathbb{E}(S)=L^n+\mathbb{E}(S').$ So $\mathbb{E}(\text{first }66) = 6^2 + \mathbb{E}(\text{first }6) = 36 + 6 = 42.$
Solution 6
$\displaystyle M=\left( \begin{array}{ccc} \frac{5}{6} & \frac{1}{6} & 0 \\ \frac{5}{6} & 0 & \frac{1}{6} \\ 0 & 0 & 1 \\ \end{array} \right)$
$\displaystyle M'_n=(1,0,0).\bf{M}^n=\left( \begin{array}{c} \frac{2^{-2 n-1} 3^{-n-1} \left(\left(5+3 \sqrt{5}\right)^{n+1}-\left(5-3 \sqrt{5}\right)^{n+1}\right)}{\sqrt{5}} \\ \frac{3^{-2 n-1} 4^{-n} \left(\left(15+9 \sqrt{5}\right)^n-\left(15-9 \sqrt{5}\right)^n\right)}{\sqrt{5}} \\ \frac{1}{5}\small{2^{-2 n-1} 3^{-n-1} \left(5\ 2^{2 n+1} 3^{n+1}+\left(7 \sqrt{5}-15\right) \left(5-3 \sqrt{5}\right)^n-\left(15+7 \sqrt{5}\right) \left(5+3 \sqrt{5}\right)^n\right)}\\ \end{array} \right)$
We take the third row and get $\varphi(t)$ the PDF of the stopping time with the difference of the third rows of $M'_{n}$ and $-M'_{n-1}$:
$\displaystyle \varphi(t)=\frac{1}{\sqrt{5}}2^{-2 t-1} 3^{-t-2} \left(\left(3 \sqrt{5}+5\right)^t-\left(5-3 \sqrt{5}\right)^t\right)$
$\displaystyle\begin{align}\mathbb{E}(n)&=\sum_{t=2}^n t \varphi(t)\\ &=\frac{1}{5} 2^{-2 n-1} 3^{-n-1} \bigg(-\left(7 \sqrt{5}+15\right) n \left(3 \sqrt{5}+5\right)^n-6 \left(47 \sqrt{5}+105\right) \left(3 \sqrt{5}+5\right)^n\\ &\qquad+\left(7 \sqrt{5}-15\right) n \left(5-3 \sqrt{5}\right)^n+6 \left(47 \sqrt{5}-105\right) \left(5-3 \sqrt{5}\right)^n+35\ 3^{n+2} 4^{n+1}\bigg)\end{align}$
$\displaystyle \lim_{n\to \infty }\mathbb{E}(n)=42.$
Generalization
Number of step to $k$ 6s in a row is
$\displaystyle \mathbb{E}(n,k)=\frac{1}{p^k}+\frac{1}{p^{k-1}}+\frac{1}{p^{k-2}}+\ldots+\frac{1}{p},$
with $\displaystyle p=\frac{1}{6}.$
Acknowledgment
This is a problem from P. Nahin's Will You Be Alive 10 Years from Now? (Princeton University Press, 2014, 54-55)
Solution 2 is by Christopher D. Long; Solution 3 is by Alejandro Rodríguez; Solution 4 is by Issam Eddine; Solution 5 is by Michael Wiener; Solution 6 is by N. N. Taleb.
|Contact| |Front page| |Contents| |Probability|
Copyright © 1996-2018 Alexander Bogomolny71549074
