Segment Trisection: What Is It About?
|
| Buy this applet What if applet does not run? |
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
Segment Trisection
The applet suggests the following statement:
| From a point T on the base AB of ΔABC draw lines parallel to the medians AMa and BMb. Let D and H be the points of intersection of those lines with AC and BC, respectively. Then the medians AMa and BMb trisect the segment DH. |
| Buy this applet What if applet does not run? |
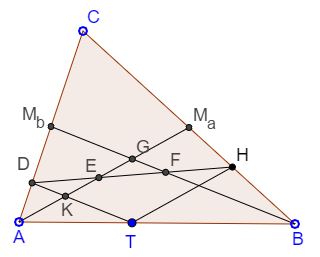
Proof
Let the notations be as in the diagram. In particular, G denotes the centroid of the triangle. This implies
| (1) | GMb = BMb / 3. |
Next note that similar triangles ABMb and ATD are divided by the median AMa into two pairs of similar triangles, from which with the help of (1)
| (2) | DK = DT / 3. |
Now, triangles DTH and DKE are also similar, so that (2) implies
| (3) | DE = DH / 3. |
Similarly, EH = DH/3. Therefore, DE = EF = FH.
|Activities| |Contact| |Front page| |Contents| |Geometry| |Store|
Copyright © 1996-2012 Alexander Bogomolny
| 41143781 |
