Nagel Point: What Is It About?
A Mathematical Droodle

---

If you are reading this, your browser is not set to run Java applets. Try IE11 or Safari and declare the site https://www.cut-the-knot.org as trusted in the Java setup.

---

What if applet does not run?

Explanation

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny

The applet may suggest the following statement:

Let E, D, F be the points of tangency of the excircles of ΔABC and its sides, as in the applet below. Prove that AD, BE, CF are concurrent. The point of concurrency is known as the Nagel point of ΔABC.

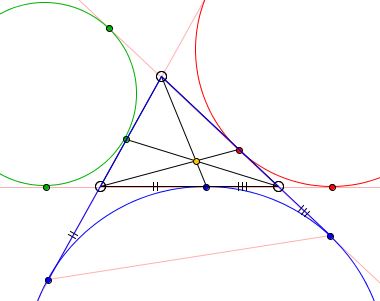
The proof relies on Ceva's theorem.

First, let C_C denote the excircle of ΔABC opposite the vertex C. C_C is tangent to the side AB and the side lines AC and BC in points F, T and U. Since, CT and CU are the two tangents from C to C_C, they are equal in length:

(1)

CT = CU.

For a similar reason

(2)

AT=AF.

(3)

BU = BF.

(1)-(3) immediately imply that F is a perimeter splitter in the sense that

AC + AF = BC + BF.

If a, b, c are the side lengths of the ΔABC and p its semiperimeter in a standard way, then this fact could be rewritten as

b + AF = a + BF = p,

so that

AF = p - b
BF = p - a.

Similarly, we obtain additional four identities:

AE = p - c
CE = p - a
CD = p - b
BD = p - c.

Ceva's identity is then verified directly:

AE/CE·CD/BD·BF/AF = (p-c)/(p-a)·(p-b)/(p-c)·(p-a)/(p-b) = 1.

(A curious fact is that these same points D, E, F arise in a related, yet quite a different construction.)

Related material Read more...
	Incircles and Excircles in a Triangle
	Nagel Point of the Medial Triangle
	Homothety between In- and Excircles
	Property of Points Where In- and Excircles Touch a Triangle
	Feuerbach's Theorem: A Proof
	Feuerbach's THeorem: What Is It?

|Activities| |Contact| |Front page| |Contents| |Geometry|

Copyright © 1996-2018 Alexander Bogomolny