Scrub Tile Puzzle
Place (by dragging) the ten words at the bottom of the applet into the ten cells that form a chain such that any two words adjacent in the chain, share one common letter.
| What if applet does not run? |
The puzzle comes in two variants [Rodgers] that differ from one another ever so slightly. The words SON, HUT in one are replaced with SUN, HOT in the other. Try both of them.
|Contact| |Front page| |Contents| |Algebra| |Eye opener|
Copyright © 1996-2018 Alexander Bogomolny
Discussion
Of the two variants of the puzzle, the second is solvable, the first is not. The reason is that the two variants are represented by different graphs:
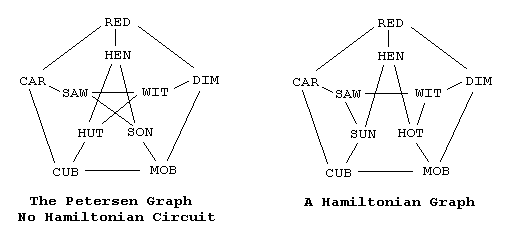
Obviously, a solution to the puzzle constitutes a Hamiltonian circuit on its graph. (A circuit in a graph is Hamiltonian if it passes through every node of the graph exactly once.) The first of the two is the famous Petersen graph that is known not to house any Hamiltonian circuits. In the second, Hamiltonian circuits are easily found even by trial and error. (M. Gardner's The Last Recreations contains a chapter on the Pigeonhole Principle and a chapter on Snarks that can't live without the Petersen graph.) A generalized version of the Pigeonhole is naturally used to show that the Petersen graph does not have Hamiltonian circuits.
The inventor, Tom Rodgers, suggests using the puzzle to amuze oneself at the expense of befuddled friends. Have 12 word scrub tiles ready and use 10 of them to arrange publicly in a chain. Then drop the tiles on the table. "Be careful to hold onto the HOT and SUN scrub with your thumps, letting HUT and SON fall in their place. Your poor, befuddled victim will have no chance at finding a loop."
References
- Tom Rodgers, A Scrub Tile Puzzle, in Puzzler's Tribute, D. Wolfe and T. Rodgers (eds.), A K Peters, 2002
Related material
| |
Math Curiosities | |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
|Contact| |Front page| |Contents| |Algebra| |Eye opener|
Copyright © 1996-2018 Alexander Bogomolny
71752804
