Similar Triangles And More

|
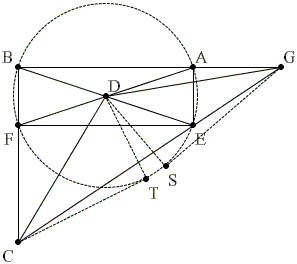
Let ABFE be a rectangle and D be the intersection of the diagonals AF and BE. A straight line through E meets the extended line AB at G and the extended line BF at C so that
| AB/CF = CF/AG = AG/AE. |
References
- T. Tao, Solving Mathematical Problems, Oxford University Press, pp. 55-58
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny

|
Proportions bring to mind similar triangles of which three are prominent: BCG, FCE, and AEG. Since ABFE is a rectangle,
| AB/CF = EF/CF = AG/AE. |
Thus two of the ratios in the problem are indeed equal. Furthermore, they are equal without the imposed condition
| (1) | CD = DG. |
Unless that condition is superfluous, we will need it for proving that the third (middle) ratio equals the other two. Before we use it, note that bringing in the third triangle (BCG) we obtain, for example,
| AG/AE = BG/BC. |
This must be equal to the middle ratio, CF/AG, which would be equivalent to
| (2) | BG·AG = BC·CF. |
The left product appears in the statement of the power of a point theorem for G with respect of the circumcircle of ABFE. Similarly, the right product appears in the statement of the power of a point theorem for C with respect to the same circle.
|
This immediately shows how to employ the special condition (1). Due to (1), points C and G are equidistant from the center of the circle and, therefore, the tangents from C and G to the circle are equal. This tells us that their powers with respect to the circle are equal. Thus (2) is indeed correct, and all three ratios are equal, as required.
|Up| |Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny
71549929
