A Characteristic Property of Centroid

In ΔABC, a line is drawn through centroid G. Assume the line intersects AB in M and AC in N. Then

(1) BM/MA + CN/NA = 1.

Here, BM, MA, CN, NA are considered as signed segments. In a certain sense the identity even holds when the line in question is parallel to, say, AB. In this case, M is a point at infinity and BM/MA = -1 whereas CN/NA = 2. Conversely, if any line through a point P satisfies (1), then necessarily P = G.

Proof.

Proof

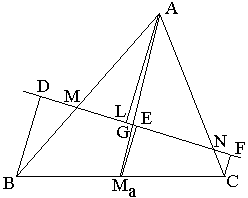
Let M_a be the midpoint of side BC. Drop perpendiculars BD, M_aE, and CF onto the given line. Obviosly

(2)	M_aE = (BD + CF)/2.

Let also AL be perpendicular to MN. Triangles ALG and M_aEG are similar and GA = 2·M_aG. Therefore, LA = 2M_aE, or

(2')	LA = BD + CF.

Triangles BDM and ALM are similar, as are triangles CFN and ALN, from where we get

BM/MA + CN/NA	= BD/LA + CF/LA
	= (BD + CF)/LA
	= LA/LA (from 2')
	= 1.

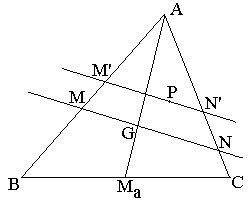
Let's now tackle the converse. Assume point P is such that

(1')	BM'/M'A + CN'/N'A = 1

holds for any line through P that intersects AB in M' and AC in N'. We have to show that P = G.. To this end assume that P is different from G and that the line is different from GP. Let MN passes through G parallel to M'N'. Then, with the reference to the diagram above,

(3)

BM/MA + CN/NA

< BM'/M'A + CN'/N'A.

This is because, in the diagram, BM/MA < BM'/M'A and CN/NA < CN'/N'A. For other locations of P or the straight line, the inequalities may have to be simultaneously reversed. (3) implies

BM/MA + CN/NA < 1,

which contradicts the proven part.

40585906