Josephus Flavius Problem
Recursive Solution

A recent letter from a math teacher reminded my that the recursive solution I have been planning to describe for a while now is long overdue.

This solution applies to the case where every other person is executed (m = 2) until only one is left (r = 1, see the complete solution.)

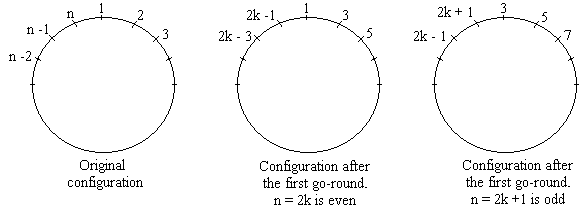
After the first go-round we essentially come up with the same problem but for a different number of individuals. We have to distinguish between two cases: n is even and n is odd. When n is even, n = 2k, k fellows remain and on the second round we start with the one who was initially number 1. When n is odd, n = 2k + 1, just before ending the first round, we get to pick out number 1; so that number 3 becomes the next victim. On the first round we eliminate k + 1 people. In both cases, k people remain for the second round. The second round is very much like the first one, except that each person's number has been doubled and, in the first case, decreased by one, while, in the second, it was increased by one. Let J(n) denote the survivor's number. Obviously, J(1) = 1. For other n, we can write

There is a way to solve these recursive formulas but the result is simple enough for us just to guess the right expression. The formulas are very easy to apply. Let's build a table for the first few values of n:

We may now notice that J(n) is always odd and starts anew from 1 with every power of 2. It increases through all successive odd numbers until it is about to reach the next power of 2 when it again drops to 1. For every number n, there exists an integer a such that 2^a ≤ n < 2^{a + 1}. For some 0 ≤ t < 2^a then n = 2^a + t. From the table above we may surmise the formula

J(2^a + t) = 2t + 1.

We prove the formula by induction on a. For a = 1 the only admissible value of t is 0 and we only have to verify that J(1) = 1 which we know to be true. For the induction step, we assume that the formula holds for all a up to a certain value. Now consider this value of a. The induction step has two parts, depending on whether n (and thus t) is even or odd. If 2^a + t = 2k, then

J(2^a + t) = 2J(2^{a -1} + t/2) - 1 = 2(2t/2 + 1) - 1 = 2t + 1

by the inductive assumption. Similarly, if 2^a + t = 2k + 1, then

J(2^a + t) = 2J(2^{a -1} + (t-1)/2) + 1 = 2(2(t-1)/2 + 1) + 1 = 2t + 1

This completes the induction step.

Reference

1. R. Graham, D. Knuth, O. Patashnik, Concrete Mathematics, 2nd edition, Addison-Wesley, 1994.

• Josephus Flavius problem
• Two ancient variants
• A simple solution
• Partial recursive solution
• A problem from USAMTS

|Contact| |Front page| |Contents| |Games|

Copyright © 1996-2018 Alexander Bogomolny