Carnot's Theorem
Lazare Nicolas Marguérite Carnot (1753-1823) was a person of many gifts and strong political views. During the Revolution he directed the Army of the North and under Napoleon Bonaparte he served as the Minister of War. In 1794, together with Gaspard Monge he founded the now famous Ecole Polytechnique. His geometric and military publications are considered masterpieces in their respective areas.
The nice little theorem that bears his name shows an unexpected relationship between the radii of the circumcircle and incircle of a given triangle.
In the formulation and the proof of Carnot's theorem I'll use the standard notations. The theorem read as follows
In any $\Delta ABC,\,$ the (algebraic) sum of the distances (suitably signed) from the circumcenter $O\,$ to the sides, is $R + r,\,$ the sum of the circumradius and the inradius.
$OM_{a} + OM_{b} + OM_{c} = R + r.$
In acute triangles, the circumcenter is always located inside the triangle. In this case, all three segments $OM_{a},\,$ $OM_{b},\,$ and $OM_{c}\,$ lie entirely inside the triangle. If one of the angles is obtuse, the circumcenter falls outside the triangle. One of the segments (the one that corresponds to the side opposite the obtuse angle) lies entirely outside, while the other two segments lie only partially outside the triangle. In the above sum, the segments that intersect the interior of the triangle are taken with the sign $plus,\,$ the remaining side with the sign $minus.\,$ Segments $OM_{a},\,$ $OM_{b},\,$ and $OM_{c}\,$ serve as altitudes of triangles $OBC,\,$ $OAC,\,$ and $OAB\,$ with the bases on the sides $a,\,$ $b,\,$ and $c.\,$ The sign convention guarantees that the areas of these triangles (taken with the proper signs) always add up to the area of $\Delta ABC.\,$

Proof 1
I shall consider only the case of an acute triangle. The other case is left as an exercise.
For the inradius we always have
$r(a + b + c) = 2Area(ABC).$
From the above, we also have $Area(OAB) + Area(OBC) + Area(OAC) = Area(ABC).\,$ Therefore,
| (*) | $r(a + b + c) = aOM_{a} + bOM_{b} + cOM_{c}.$ |
A remark is now in order. $O\,$ being the circumcenter of $\Delta ABC,\,$ in the isosceles triangle $AOB,\,$ $\angle AOB = 2\angle C.\,$ And similarly, $\angle BOC = 2\angle A\,$ and $\angle AOC = 2\angle B.\,$ Equipped with this knowledge we may consider several triples of similar (right-angled) triangles:
- $ABH_{b},\,$ $ACH_{c},\,$ and $BOM_{a}\,$ (or, an equal $COM_{a})$
- $BAH_{a},\,$ $BCH_{c},\,$ and $COM_{b}\,$ (or, an equal $AOM_{b})$
- $CBH_{b},\,$ $CAH_{a},\,$ and $AOM_{c}\,$ (or, an equal $BOM_{c})$
From the first triple we derive
$AH_{b}/c = AH_{c}/b = OM_{a}/R$
which leads to
$OM_{a}(b + c) = R(AH_{b} + AH_{c})$
Similarly, we get two additional identities
$OM_{b}(a + c) = R(BH_{a} + BH_{c})\\ OM_{c}(a + b) = R(CH_{a} + CH_{b})$
Summing the three up yields after simplifications
$OM_{a}(b + c) + OM_{b}(a + c) + OM_{c}(a + b) = R(a + b + c).$
Adding this to (*) and dividing by $(a + b + c)\,$ completes the proof.
Proof 2
Below I'll refer to a modified diagram that necessitates a change in notations. The proof is by Vaggelis Stamatiadis.
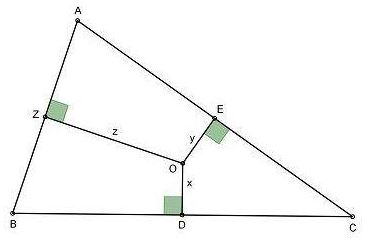
Quadrilaterals $AZOE,\,$ $BDOZ,\,$ $CEOD\,$ are cyclic, allowing for an application of Ptolemy's theorem:
$OD\cdot BZ+OZ\cdot BD=OB\cdot DZ\\ OZ\cdot AE+OE\cdot AZ=OA\cdot EZ\\ OE\cdot DC+OD\cdot EC=OC\cdot DE,$
which can be written as
$\displaystyle\begin{align} x\frac{c}{2}+z\frac{a}{2}&=R\frac{b}{2},\\ z\frac{b}{2}+y\frac{c}{2}&=R\frac{a}{2},\\ y\frac{a}{2}+x\frac{b}{2}&=R\frac{c}{2}, \end{align}$
or,
$\displaystyle x(b+c)+y(c+a)+z((a+b)=R(a+b+c)\,\Longleftrightarrow\\ x(2s-a)+y(2s-b)+z(2s-c)=2sR\,(2s=a+b+c)\,\Longleftrightarrow\\ 2s(x+y+z)-(ax+by+cz)=2sR\,\Longleftrightarrow\\ 2s(x+y+z)-2[\Delta ABC]=2sR\,\Longleftrightarrow\\ 2s(x+y+z)-2sr=2sR\,\Longleftrightarrow\\ x+y+z=R+r.$
If, say, the angle at $A\,$ is obtuse, the relationship becomes $y+z-x=R+r.$
References
- R. Honsberger, Mathematical Gems III, MAA, 1985
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
73560447
