Stathis Koutras' Theorem
Problem
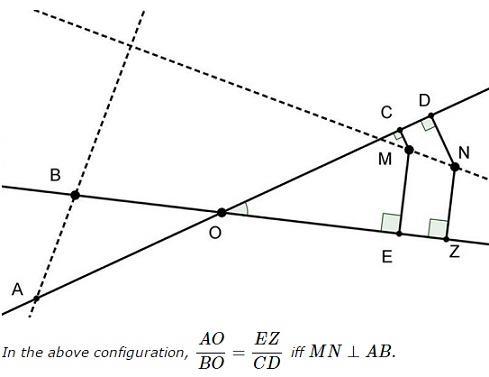
Solution 1
Choose $O=(0,0),\,$ $OE:\;y=0;\,$ $OC:\;y=mx,\,$ with $m\gt 0;\,$ $E=(u,0),\,$ with $u\gt 0,\,$ $Z=(v,0),\,$ with $v\gt 0,\,$ $C=(w,mw),\,$ with $w\gt 0,\,$ and $D=(t, mt),\,$ with $t\gt w.\,$ The interior of $\angle COD\,$ is defined by the double inequality $0\lt y\lt mx.\,$ We have
$\displaystyle\begin{align} &ME:\;x=u,\,MC:\;x+my=w(1+m^2)\;\Rightarrow\\ &\qquad\qquad\qquad M=\left(u,\frac{w(1+m^2)-u}{m}\right),\,\frac{u}{1+m^2}\lt w\lt u.\\ &NZ:\;x=v,\,ND:\;x+my=t(1+m^2)\;\Rightarrow\\ &\qquad\qquad\qquad N=\left(v,\frac{t(1+m^2)-v}{m},\right),\,\frac{v}{1+m^2}\lt t\lt v. \end{align}$
The slope of $MN\,$ is $\displaystyle\frac{(t-w)(1+m^2)-(v-u)}{m(v-u)}.\,$ Also, $\displaystyle\frac{EZ}{CD}=\frac{v-u}{(t-w)\sqrt{1+m^2}}.\,$
Let $A=(-a,-ma),\,$ $B=(-b,0),\,$ with $a,b\gt 0.\,$ We then have $\displaystyle\frac{OA}{OB}=\frac{a\sqrt{1+m^2}}{b};\,$ the slope of $AB\,$ is $\displaystyle -\frac{ma}{b-a}.\,$ Thus, $\displaystyle\frac{OA}{OB}=\frac{EZ}{CD}\,$ which is equivalent to
$\displaystyle\frac{a\sqrt{1+m^2}}{b}=\frac{v-u}{(t-w)\sqrt{1+m^2}},$
or $a(t-w)(1+m^2)=b(v-u).\,$ Additionally, $AB\perp MN,\,$ is equivalent to
$\displaystyle\frac{(t-w)(1+m^2)-(v-u)}{m(v-u)}=\frac{b-a}{ma},$
which is equivalent to $a(t-w)(1+m^2)=b(v-u).\,$ This completes the proof.
Solution 2
Stathis Koutras
16 December, 2011
Translation by Takis Chronopoulos
Source
Given two lines $(x),(y)\,$ intersecting at a point $O.\,$ Let $A\in (x),\,B\in (y),\,$ with $A\ne O\ne B.\,$ Segment $MN\,$ of length $a\,$ has projections $a_x\,a_y\,$ on lines $(x),(y)\,$ respectively. Prove that if $\displaystyle\frac{OA}{a_y}=\frac{OB}{a_x},\,$ then $MN\perp AB.$
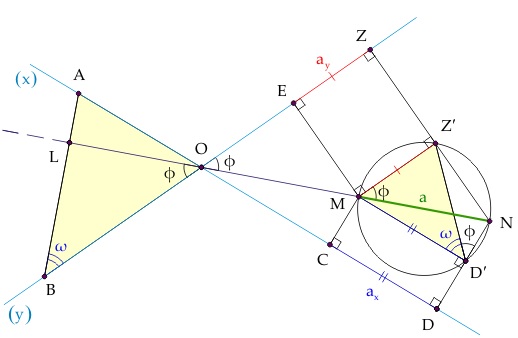
Without loss of generality assume that the line $MN\,$ passes though $O\,$ (because the projections of equal and parallel segments on given sides are equal.)
Let $MC\perp (x),\,$ $ND\perp (x)\,$ so that $CD=a_x,\,$ and $ME\perp (y),\,$ $NZ\perp (y)\,$ so that $EZ=a_y.$
If $MZ'\parallel (y),\,(Z'\in DZ),\,$ and $MD'\parallel (x),\,$ $(D'\in ND)\,$ then obviously from the constructed rectangles:
(1)
$MD'=CD=a_x,\,$ $MZ'=EZ=a_y.\,$
Also:
(2)
$\displaystyle\angle D'MZ'\overset{parallel\,sides}{=}\angle ZOD\overset{vertical}{=}\angle AOB.$
From the assumption it follows that
$\displaystyle\frac{OA}{a_y}=\frac{OB}{a_x}\overset{(1)}{\Rightarrow}=\frac{OA}{MZ'}=\frac{OB}{MD'}\overset{(2)}{\Rightarrow}\Delta MD'Z' \sim\Delta OAB$
and, as a consequence,
(3)
$\angle MD'Z'=\angle OBA.$
Also, $\displaystyle\angle LOB\overset{vertical}{=}\angle NOZ\overset{corresponding}{=}\angle NMZ',\,$ so that
(4)
$\angle LOB=\angle NMZ'.$
Obviously the quadrilateral $MZ'ND'\,$ is cyclic: $\angle MZ'N+MD'N=90^{\circ}+90^{\circ}.\,$ Therefore, $\angle NMZ'=\angle ND'Z',\,$ implying by (4)
(5)
$\angle LOB=\angle ND'Z'.$
Finally,
$\displaystyle\angle LOB+\angle OBA\overset{(3),(5)}{=}\angle ND'Z'+MD'Z'=MD'N\overset{MD'\perp ND}{=}90^{\circ},$
so that
$\displaystyle\angle LOB+\angle OBA=90^{\circ}\overset{\Delta LOB}{\Rightarrow}\angle OLB=90^{\circ}\Rightarrow MN\perp AB.$
Solution 3
Kostas Vittas
7 August, 2013
Translation by Takis Chronopoulos
Source
Koutras' Theorem
Given angle $\angle xOy\,$ and let $M\,$ and $N,\,$ be random interior points. Let $C,D\,$ be the projections of $M,N\,$ respectively, on $Ox\,$ and $E,Z\,$ their projections on $Oy,\,$ respectively. On $Ox,Oy,\,$ or on their extensions towards $O,\,$ we consider the points $A,B,\,$ respectively, so that $\displaystyle\frac{OA}{OB}=\frac{EZ}{CD}.\,$ Prove that $MN\perp AB.$
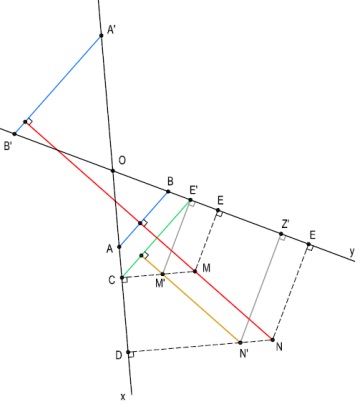
Let $E'\,$ be a point on $Oy\,$ such that $CE'\parallel AB\,$ and let points $M',N',Z'\,$ on $MC,ND,Oy,\,$ respectively, be such that $M'E'\parallel ME,\,$ $M'N'\parallel MN,\,$ and $N'Z'\parallel NZ.\,$ Now, $CE'\parallel AB\,$ implies
(1)
$\displaystyle\frac{OA}{OB}=\frac{OC}{OE'}.$
Also, $M'N'\parallel MN\,$ implies
(2)
$E'Z'=EZ.$
From (1), (2), and $\displaystyle\frac{OA}{OB}=\frac{EZ}{CD},\,$ it follows that
(3)
$\displaystyle\frac{OC}{OE'}=\frac{E'Z'}{CD}.$
From (3), according to the lemma below, it follows that
(4)
$M'N'=CE'.$
From (4) and $M'N'\parallel MN,\,$ $CE'\parallel AB,\,$ we conclude that $MN\perp AB,\,$ competing the proof.
Lemma
On the extensions of sides $AB,AC,\,$ of a given $\Delta ABC,\,$ towards $B,C,\,$ we consider points $D,E,\,$ respectively, so that $\displaystyle\frac{AB}{AC}=\frac{CE}{BD}.\,$ The perpendicular lines from $B,C,\,$ on $AB,AC,\,$ respectively, intersect at a point $P;\,$ and let $Q,\,$ be the intersection of the perpendiculars from $D,E\,$ on $AD,AE,\,$ respectively. Prove that $PQ\perp BC$.

Proof of Lemma
Let $D',E',\,$ be the projections of point $P\,$ on $QD,QE,\,$ respectively. From $PD'\parallel =BD\,$ and $PE'\parallel =CE,\,$ it follows that $\angle D'PE'=\angle BAC.\,$ And from the similarity of triangles $ABC\,$ and $PE'D',\,$ due to $\displaystyle\frac{AB}{AC}=\frac{CE}{BD},\,$ it follows that $\displaystyle\frac{AB}{AC}=\frac{PE'}{PD'}\,$ and, further, $\angle ABC=\angle PE'D'.\,$ Now, since quadrilateral $PE'QD'\,$ is cyclic $(\angle PD'Q=\angle PE'Q=90^{\circ})\,$ $\angle PE'D'=\angle PQD',\,$ so that also $\angle ABC=\angle PQD'.\,$ From that it follows that the quadrilateral $BDQT,\,$ where $T=BC\cap PQ,\,$ is cyclic and, therefore, $\angle BTQ=\angle BDQ=90^{\circ},\,$ i.e., $PQ\perp BC,\,$ as required.
Solution 4
Grégoire Nicollier
4 January, 2017
The vector $\overrightarrow{NM}\,$ can be translated to $O\,$ as the origin while its projections remain unchanged. Under such a translation points $Z,D,N\,$ collapse onto $O.\,$ I'll use $N\,$ to refer to all four so that $CD\,$ becomes $CN\,$ and $EZ\,$ becomes $EN;\,$ $AO\,$ and $BO\,$ are $AN\,$ and $BN,\,$ respectively. The theorem states that
$\displaystyle \frac{AN}{BN}=\frac{EN}{CN}\,$ iff $MN\perp AB.$
Now, $NM\,$ can be considered as a side of a triangle $MNP\,$ with side $NP\,$ along $NB\,$ and an altitude along $NA.\,$
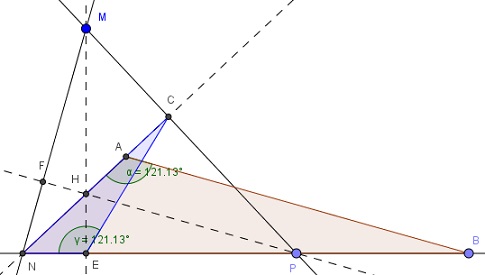
$AN\,$ and $BN\,$ form triangle $ABN;\,$ $EN\,$ $CN\,$ form triangle $ENC.\,$ As a matter of fact, this two triangles are always similar if $MN\perp AB\,$ which establishes the required proportion. To see why it is so, draw the altitudes and the orthocenter $H\,$ of $\Delta MNP.\,$ $NC\,$ is already present, $ME\,$ is another one, and let $PF\,$ be the third. In particular, $PF\parallel AB.$
Further, $\angle NAB=\angle NHP=180^{\circ}-\angle NMP\,$ because $CHFM\,$ is a cyclic quadrilateral. On the other hand, $CE\,$ is known to be an antiparallel to $MN,\,$ so that $\angle CEP=\angle NMP,\,$ making $\angle NEC=\angle NHP.\,$ The two triangles also share $\angle CNP.\,$ So, finally, $\Delta ABN\sim\Delta ENC,\,$ as expected. (A shorter way to arrive at the same conclusion is by noticing that the quadrilateral $HCEP\,$ is cyclic which shows $\angle NCE=\angle NPM.)$
Solution 5
Nguyen Van Loi
6 January, 2017
Source
Draw a line through $O\,$ parallel to $MN.\,$ Let it intersect $AB\,$ at $T.\,$
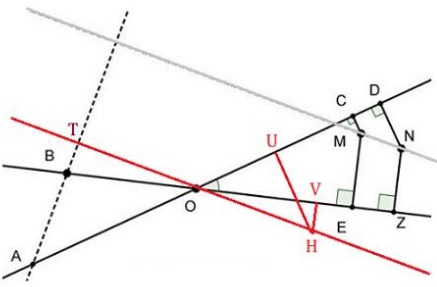
Choose an arbitrary point $H\,$ on that line and drop perpendiculars $HV\,$ and $HU\,$ on $OB\,$ and $OA,\,$ respectively. Then $\displaystyle\frac{AO}{BO}=\frac{EZ}{CD}=\frac{OV}{OU},\,$ i.e., $AO\cdot OU=OH\cdot OT=OB\cdot OV.$
Solution 6
Sotirios Louridas
1 January, 2017
Translation by Takis Chronopoulos
Source
In the following figure we consider $)A_1=EZ,$ and $OB_1=CD,\,$ so that, since $OT\,$ and $MN\,$ have equal projections in respect to the same lines we also have $OT=MN.$
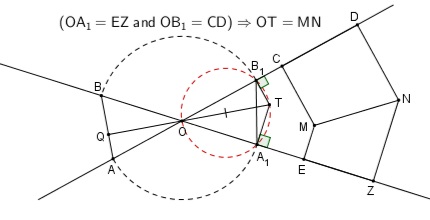
From $\displaystyle\frac{OA_1}{OB_1}=\frac{EZ}{CD}=\frac{OA}{OB},\,$ it follows that triangles $OA_1B_1\,$ and $OAB\,$ are similar. In particular, $\angle OAB=B_1A_O.\,$ Define $Q\,$ as the intersection of $TO\,$ and $AB.\,$
(1)
$\angle QOA+\angle OAB=\angle TOB_1+\angle B_1A_1O.$
In cyclic quadrilateral $OA_1TB_1,$
(2)
$\angle TOB_1=\angle TA_1B_1.$
From (1) and (2),
$\angle QOA+\angle OAB=\angle TA_1B_1+\angle B_1A_1O=90^{\circ},$
implying $TO\perp AB.$
In the opposite direction:
Le $Q\,$ be the intersection of $TO\,$ with $AB\,$ and $OQ\perp AB.\,$ Triangles $OQA_1,\,$ $OTB_1\,$ are similar, making $\angle OAB=\angle B_1TO=\angle BA_1O.\,$ Thus triangles $OAB\,$ and $OA_1B_1\,$ are also similar, implying $\displaystyle\frac{OA}{OB}=\frac{OA_1}{OB_1}=\frac{EZ}{C}.$
Solution 7
Mihalis Lambrou
1 January, 2017
Translation by Takis Chronopoulos
Source
WLOG, assume $MN\,$ passes through $O.$
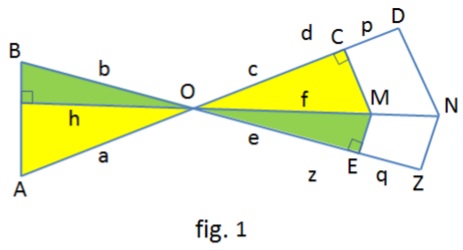
From the similar yellow triangles we have $\displaystyle\frac{a}{h}=\frac{f}{c}.\,$ From the green triangles, $\displaystyle\frac{h}{b}=\frac{e}{f}.\,$ Multiplying we have $\displaystyle\frac{a}{b}=\frac{e}{c}.\,$ Similarly $\displaystyle\frac{a}{b}=\frac{z}{d}.\,$ Therefore,
$\displaystyle\frac{a}{b}=\frac{e}{c}=\frac{z}{d}=\frac{z-e}{d-c}=\frac{p}{q},$
as desired.
Converse:
We draw from $A\,$ $AB'\,$ perpendicular to $MN.\,$

From the hypothesis and above, we have $\displaystyle\frac{a}{b}=\frac{p}{q}=\frac{a}{b'},\,$ implying $b=b'\,$ and so points $B\,$ and $B'\,$ coincide. Etc.
Solution 8
Evaggelos Taratoris
2 January, 2017
Translation by Takis Chronopoulos
Source
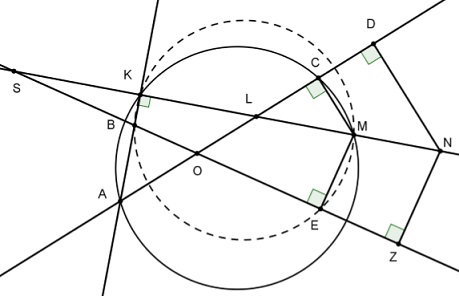
Converse:
Let $MN\,$ be perpendicular to $AB.\,$ Let $L,S\,$ be the intersections of $MN\,$ with $AO\,$ and $BO,\,$ respectively. Then $\displaystyle\frac{SE}{EZ}=\frac{SM}{MN}\,$ and $\displaystyle\frac{LM}{MN}=\frac{LC}{CD}\,$ due to parallelism. It follows that
(1)
$\displaystyle\frac{EZ}{CD}=\frac{SE}{SM}\cdot\frac{LM}{LC}.$
From cyclic quadrilaterals $KMEB\,$ and $CMAK,\,$ we have $SK\cdot SM=SB\cdot SE\,$ and $LM\cdot LK\,$ and $LC\cdot LA.\,$ Thus, (1) becomes
(1')
$\displaystyle\frac{EZ}{CD}=\frac{SK}{SB}\cdot\frac{LA}{LK}.$
By Menelaus' Theorem in $\Delta OLS,\,$ and transversal $ABK,\,$ $\displaystyle\frac{OA}{LA}\cdot\frac{LK}{SK}\cdot\frac{SB}{BO}=1,\,$ and subsequently, $\displaystyle\frac{OA}{OB}\cdot\frac{CD}{EZ}=1,\,$ which concludes the proof.
Solution 9
Antreas Varverakis
4 January, 2017
Translation by Takis Chronopoulos
Source

We let segments, $EZ,\,$ $CD\,$ slide on the two lines, until they have the same end point $O.\,$ On the respective perpendiculars, construct a parallelogram $MLNU\,$ which remains unchangeable during movement, since its sides have common direction and its heights constant length. Therefore, the diagonal $MN\,$ maintains constant direction.
In the constructed triangle $OXK,\,$ $H\,$ is the orthocenter, therefore, $OH\perp KX.\,$ But, $KX/parallel AB,\,$ for, from the similar triangles $OPX\,$ and $ORK,\,$ we have:
$\displaystyle\frac{OB}{OA}=\frac{CD}{EZ}=\frac{OR}{OP}=\frac{OK}{OX},$
implying $OH\perp AB.$
Proofs 10 & 11
Solution 12
Paulos Dimos
1 January, 2017
RIP: 8 January, 2017
Translation by Takis Chronopoulos
Source
Let
(1)
$d=L\cos\omega,\,$=L\cos\varphi.$

Draw from point $O\,$ line $(e)\,$ parallel to $MN\,$ and construct segment $OT\,$ so that $OT=\lambda\cdot L\,$ by taking
$OB=OK=OT\cos\varphi=\lambda\cdot L\cos\varphi,\\ OA=OC=OT\cos\omega=\lambda\cdot L\cos\omega.$
Obviously we have $\displaystyle\frac{OA}{OB}=\frac{\lambda\cdot L\cos\omega}{\lambda\cdot L\cos\varphi}\overset{(1)}{=}\frac{d}{s}.$
Quadrlateral $OCTK\,$ is cyclic, so that
(2)
$\hat{\theta_2}=\hat{\theta_3}.$
Quadrlateral $BKTC\,$ is cyclic, so that
(3)
$\hat{\theta_2}=\hat{\theta_1}.$
Combining (2) and (3),
$\hat{\theta_1}=\hat{\theta_3}.$
Hence, $\hat{\theta_1}=90^{\circ}-\varphi,\,$ implying $AB\perp (e)\,$ and, subsequently, $AB\perp MN.$
Acknowledgment
Takis Chronopoulosc has kindly posted the above problem at the CutTheKnotMath facebook page, with a link to a post of his at the Οι Ρομαντικοι της Γεωμετριας (Romantics of Geometry) facebook group. Leo Giugiuc almost immediately replied with a solution of his (Solution 1). Solution 2 by Stathis Koutras; Solution 3 by Kostas Vittas; Solution 4 is by Grégoire Nicollier; Solution 5 is by Nguyen Van Loi; Solution 6 is by Sotirios Louridas; Solution 7 is by Mihalis Lambrou; Solution 8 is by Evaggelos Taratoris; Solution 9 is by Antreas Varverakis; Solutions 10&11 are by Stathis Koutras.
All translations from Greek are by Takis Chronopoulos.
Mote that one of the proofs is incorrect. It assumes that which has to be proved.
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73653813
