Conics Related To In- and Excircles
What is this about?
Problem
The points of tangency of the excircles on the extensions of the sides of a triangle lie on a conic. So do the points of tangency of the incircle and excircles on the sides proper:
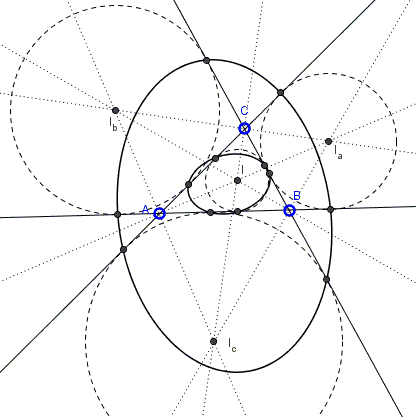
Hint
These are rather obvious applications for Carnot's Theorem.
Solution
For a proof I shall simply refer to the diagram below, with the segment lengths derived on a separate page:
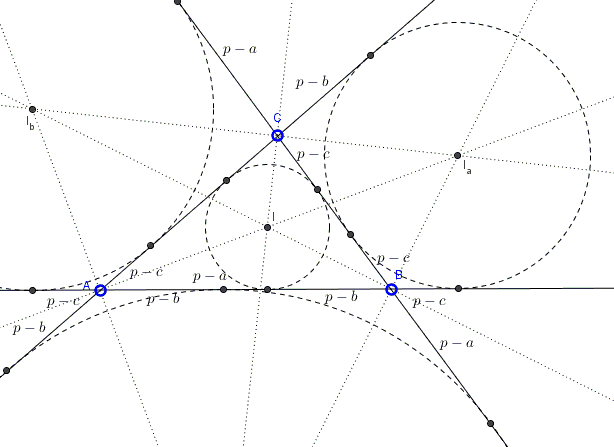
Carnot's criterion
\(\displaystyle \bigg(\frac{AC_a}{BC_a}\cdot\frac{AC_b}{BC_b}\bigg)\cdot\bigg(\frac{BA_b}{CA_b}\cdot\frac{BA_c}{CA_c}\bigg)\cdot\bigg(\frac{CB_c}{AB_c}\cdot\frac{CB_a}{AB_a}\bigg)=1. \)
for the six tangencies of the excircles on the side extensions appears as
\(\displaystyle \bigg(\frac{p-c}{p}\cdot\frac{p}{p-c}\bigg)\cdot\bigg(\frac{p-a}{p}\cdot\frac{p}{p-a}\bigg)\cdot\bigg(\frac{p-b}{p}\cdot\frac{p}{p-a}\bigg)=1, \)
while the six tangencies of the incircle and the excircles on the sides proper it appears as
\(\displaystyle \bigg(\frac{p-b}{p-a}\cdot\frac{p-a}{p-b}\bigg)\cdot\bigg(\frac{p-c}{p-b}\cdot\frac{p-b}{p-c}\bigg)\cdot\bigg(\frac{p-a}{p-c}\cdot\frac{p-c}{p-a}\bigg)=1, \)
where, as usual, $p=(a+b+c)/2.$
Acknowledgment
There is a very comprehensive page at the site of Ricardo Barroso Campos devoted to the work of Lazare Carnot and, his criterion, in particular.
![]()
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny73346019
