A Minesweeper Theorem

An engaging theorem has been published by Antonio Jara del las Heras from Avila, Spain (Am Math Monthly, v 116, n 3, March 2009, p. 227). The popular Minesweeper puzzle serves as the background.

The theorem is concerned with shapes on a square grid. A board is any combination of grid squares, some of which are blank whilst some are marked with mines. Each blank square in a board is assigned a poor neighbor number, which is the number of adjacent squares of the board that carry a mine. Adjacency may be 8-adjacency, as in the original minesweeper puzzle, or 4-adjacency, or in fact, any other kind that may come to mind. The mine total of the board is the sum of all poor neighbor numbers over all blank squares in the board.

With any board we associate a complementary board which is the board of exactly the same shape, in which the previously blank squares carry a mine, and those that had a mine in them became blank. When a board is overlapped by its complement, the result is a board of the same shape with every square carrying exactly one mine.


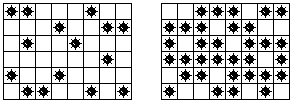
	A board and its complement

Theorem

A board and its complement have the same mine total number.

Example

For the above board and the 8-adjacency relationship, the distribution of the poor neighbor numbers is as depicted in the diagram below.


	Example

Let's count: 1×3 + 2×18 + 3×12 = 75 = 2 + 3×3 + 4×4 + 5 + 6 + 7×3 + 8×2.

Proof

The proof is based on the following obvious fact. Let A be a finite set and R a relation o A. Let B and C be any two subsets of A. Then, using |S| as the number of elements in a finite set S,

∑_x∈B|{y∈C: xRy}| = ∑_y∈C|{x∈B: xRy}|.

To make the equation self-evident, think of R as a subset of A×A. Then we are simply counting the elements of (B×C)∩R in two different ways.

To apply this fact to our puzzle, let A be the set of squares of the board, R the adjacency relation on A, B the set of mined squares and C = A - B the set of blank squares.

The result is valid for boards of arbitrary shapes (e.g. for toroidal boards) that are the union of arbitrarily shaped (not necessarily square) cells and also for any kind of adjacency that may be defined on such a board.

The following may be construed as a graphical elaboration of the proof in the conventional case of square cells and rectangular boards.

Let's join the centers of the blank squares with the centers of their poor neighbors. The poor neighbor number of a cell is the number of segments emanating from its center. Since, the segments join blank squares to their mined neighbors, each segment is counted only once. So that the total mine number of a board is simply the number of the drawn segments. But, for a board and its complement, the sets of drawn segment joints are exactly the same.


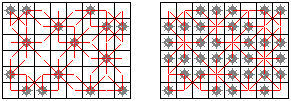
	8-adjacency on complementary minesweeper boards

71534185