Two Balls Out Of Four

Problem

balls of two colors in two bags

Solution 1

After the event $W_1$ took place, the urn contains $1$ white ball and two black balls. Thus $\displaystyle P(W_2|W_1)=\frac{1}{3}.$

The same is true of $P(W_1|W_2).$ To see that, assume the sequence of events is as follows: draw a ball blindly, place it aside, draw another ball and check its color to find it is a white ball. Now, you are permitted to check the color of the first ball. This is one ball out of three: one white, two black. The balls may be separate, but, as far as our knowledge of their colors is concerned, they are in commensurate positions. It follows that $\displaystyle P(W_1|W_2)=\frac{1}{3}.$

Solution 2

For any two events, Bayes' odds are computed according to $\displaystyle \frac{P(A|B)}{P(B|A)}=\frac{P(A)}{P(B}).$ Obviously, $\displaystyle P(W_1)=\frac{2}{4}=\frac{1}{2}.$ On the other hand, with $B$ being the event of drawing a black ball on the first draw,

$\displaystyle P(W_2)=P(W_1)\cdot\frac{1}{3}+P(B)\cdot\frac{2}{3}=\frac{1}{2}\cdot\frac{1}{3}+\frac{1}{2}\cdot\frac{2}{3}=\frac{1}{2}.$

It follows that $\displaystyle P(W_1|W_2)=P(W_2|W_1)=\frac{1}{3}.$ The difference between the two cases is purely psychological.

Solution 3

balls of two colors in two bags, NNT

Solution 4, Illustrated

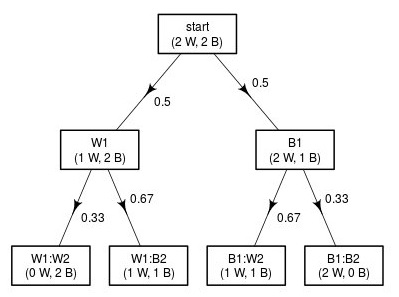
Two Balls of the Same Color, illustrated

Solution 5

Sample space (ways to draw all four balls): $BBWW,$ $BWBW,$ $BWWB,$ $WBBW,$ $WBWB,$ $WWBB.$

$\displaystyle \begin{align} &W_1=\{WBBW,WBWB,WWBB\}\\ &W_2=\{BWBW,BWWB,WWBB\}\\ &W_1\cap W_2=\{WWBB\}\\ &P(W_2|W_1)=|W_1\cap W_2|/|W_1|=1/3\\ &P(W_1|W_2)=|W_1\cap W_2|/|W_2|=1/3 \end{align}$

Acknowledgment

This is a paraphrase of problem 2.3.19 from R. Falk's Understanding Probability and Statistics (A K Peters, 1993).

Solution 3 is by N. N. Taleb; Soltution 4 is by Greg Minshall; Solution 5 is by Josh Jordan.

71549139