|
|
|
|
|
|
|
|
|
Theorem of Complete Quadrilateral: What Is It?
|
| Buy this applet |
Copyright © 1996-2008 Alexander Bogomolny
Four lines in general position (no two are parallel, no three pass through a point) define six points. The configuration of the six points and the connecting line segments that belong to the given lines is known as complete quadrilateral. In addition, the points could be split into three pairs such that the connecting segments do not belong to any of the given lines. These three segments are called diagonals of the quadrilateral.
Theorem
Midpoints of the diagonals of a complete quadrilateral lie on a line.
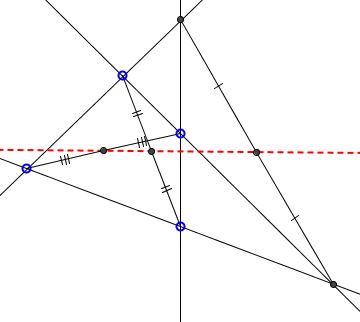
The line is commonly known as the Newton-Gauss line.
Below I give two proofs of the Theorem of Complete Quadrilateral. Before you read further, try playing with the applet. Hint #1 hints at one of the proofs, Hint #2 at the other.
| Buy this applet |
Lemma
Let in a parallelogram ABCD, lines EF and GH are parallel to the sides and meet on the diagonal AC. Then parallelograms ABEF (GBEK) and AGHD (FKHD) have equal areas. The converse is also true.
(Without the converse, the lemma is exactly Euclid I.43.)
Proof
Three pairs of triangles have equal areas: ABC and ACD, KEC and KCH, AGK and AKF. Lemma follows by comparing two algebraic sums of the areas involved.
For the converse note that if parallelograms ABEF and AGHD have equal area while lines EF and GH do not meet on the diagonal AC we may arrive at a contradiction by drawing a line parallel to AD through the intersection of EF and AC. The new parallelogram will have the area equal to that of ABEF and unequal area to that of AGHD.
The lemma is used in the first proof of the Theorem of Complete Quadrilateral.
Proof #1
Parallelograms ARCQ and APGN have equal areas, and so have ARCQ and ASTU. Therefore, the same holds for the parallelograms PGHS and HTUN. This means that H lies on AV. Therefore, midpoints of segments CV, CH and CA lie on a line (parallel to AV).
In parallelogram VBCD, the midpoint of CV coincides with the midpoint of BD, a.k.a. K. In parallelogram FHEC, the midpoint of CH coincides with that of FE, a.k.a. L.
Therefore, the three midpoints K, L, and M (of CA) lie on a line.
The second proof depends on Menelaus' theorem.
Proof #2
Choose MR||AE, KQ||BC, and LR||CD. MR||AE implies
Multiply the three proportions:
| (*) | RM/MQ · QK/KP · PL/LR = EA/AD · CB/BE · DF/FC |
Consider now two triangles and their respective transversals: triangle EDC and line AFB and triangle PRQ and line KLM - the latter is yet to be shown to be a line!
By Menelaus' theorem, the right hand side in (*) equals 1. Therefore, the product on the left is also 1. By the converse of Menelaus' theorem, the points K, L, and M lie on a line.
Remark
A stronger theorem asserts that the three circles constructed on the diagonals of a complete quadrilateral as diameters are coaxal. I.e., not only the centers of the three circles are collinear, the circles taken two by two also share the radical axis. This is known as the Gauss-Bodenmiller theorem [Treatise, p. 101].
References
- J. L. Coolidge, A Treatise On the Circle and the Sphere, AMS - Chelsea Publishing, 1971
Copyright © 1996-2008 Alexander Bogomolny
| 28735596 |  |
|