All about Symmedians

This page is intended to catalog the facts concerning symmedians in a triangle, otherwise scattered throughout this site. In a reference triangle $ABC,\;$ the symmedian $AS_{a}\;$ is a cevian through vertex $A\;$ (so that $S_{a}\;$ is a point on the side line $BC)\;$ isogonally conjugate to the median $AM_{a},\;$ $M_{a}\;$ being the midpoint of $BC.\;$ The other two symmedians $BS_{b}\;$ and $CS_{c}\;$ are defined similarly. The three symmedians $AS_{a},\;$ $BS_{b}\;$ and $CS_{c}\;$ concur in a point commonly denoted $K\;$ and variably known as the symmedian, Lemoine or Grebe's point.

$S_{a}\;$ divides $BC\;$ in the ratio

(1)

$\displaystyle\frac{BS_{a}}{S_{a}C} = \frac{c^{2}}{b^{2}}.$
It follows from Steinter's Ratio Theorem that the only point $X\;$ on the side $BC\;$ of $\Delta ABC\;$ that has the property $\displaystyle\frac{BX}{CX}=\frac{c^2}{b^2}\;$ is the foot $S_a\;$ of the symmedian through vertex $A.$
A symmedian through a vertex is the locus of the midpoints of the antiparallels to the side opposite the vertex. In particular, a symmedian splits in half a side of the orthic triangle.
For a point $P\;$ on $AS_{a},\;$ the distances $x\;$ and $y\;$ to the sides $AB\;$ and $AC\;$ are in proportion to the side lengths:

(2)

$\displaystyle\frac{x}{y} = \frac{AB}{AC}\;(= \frac{c}{b}\;$ in standard notations).

To see this, assume $S_{a}D\;$ and $S_{a}E\;$ are perpendicular to $AB\;$ and $AC,\;$ respectively. Then

$\displaystyle\begin{align} \frac{Area( \Delta AS_{a}B)}{Area( \Delta AS_{a}C)} &= \frac{AB\cdot S_{a}D}{AC\cdot S_{a}E}\\ &= \frac{BS_{a}}{S_{a}C}\\ &= \frac{AB^{2}}{AC^{2}}, \end{align}$

by (1). (2) follows directly.

The converse is also true: any point $P\;$ that satisfies the above proportion lies on $AS_{a}.$
The distance from the Lemoine point to the side lines of a triangle is proportional to the corresponding side lengths. This property uniquely determines the Lemoine point.
The Lemoine point is thus given by $a : b : c\;$ in trilinear coordinates and by $a^{2} : b^{2} : c^{2}\;$ in the barycentric coordinates.
In a right triangle, the Lemoine point coincides with the midpoint of the altitude to the hypotenuse. In particular, the altitude to the hypotenuse is also the symmedian through the right angle.
In $\Delta ABC,\;$ the antiparallels to sides $AB\;$ and $AC\;$ that meet on the symmedian from $C\;$ have equal lengths. By transitivity, the three antiparallels through the symmedian point all have equal lengths.
A symmedian through one of the vertices of a triangle passes through the point of intersection of the tangents to the circumcircle at the other two vertices. (For this reason, the symmedian always lies between the angle bisector and the altitude from the same vertex.) If $A'B'C'\;$ is the tangential triangle with $A'\;$ opposite $A,\;$ etc., then $AA',\;$ $BB',\;$ $CC'\;$ are concurrent since they serve as the symmedians of $\Delta ABC.\;$
The Lemoine point of a triangle also serves as the Gergonne point of its tangential triangle.
The Lemoine point is the center of homothety of the triangle in Grebe's construction and the reference $\Delta ABC.$
The centroid $G\;$ of the reference $\Delta ABC\;$ coincides with the Lemoine point of its antipedal triangle.
As a corollary, the Lemoine point of a triangle serves as the centroid of its pedal triangle.
The Lemoine point of the Gergonne triangle serves as the Gergonne point of the base triangle.

This is because the incircle of the base triangle is the circumcircle of the associated Gergonne triangle, so that the base triangle is the tangential triangle for the associated Gergonne triangle.
Among all points internal to $\Delta ABC,\;$ $K\;$ minimizes the sum of the squares of the distances to the sides of the triangle.

This follows immediately from the Lagrange identity:

$(a^{2} + b^{2} + c^{2})(x^{2} + y^{2} + z^{2}) = (ax + by + cz)^{2} + (bz - cy)^{2} + (cx - az)^{2} + (ay - bx)^{2}.$

Assuming, as before, that $x, y, z\;$ are the distances from a point $P\;$ to the sides of $\Delta ABC\;$ and $a, b, c,\;$ its side lengths, the quantity $ax + by + cz\;$ represents twice the area of $\Delta ABC\;$ and hence is constant. So is the quantity $a^{2} + b^{2} + c^{2}\;$. The quantity $x^{2} + y^{2} + z^{2}\;$, therefore, attains its minimum wherever $(bz - cy)^{2} + (cx - az)^{2} + (ay - bx)^{2}\;$ does. But the latter is non-negative and becomes $0\;$ for $x : y : z = a : b : c,\;$ i.e., exactly at the Lemoine point. (The requirement for $P\;$ to be internal to the triangle is easily removed by introducing signed segments and areas so that some of the terms in $ax + by + cz\;$ may be negative.)
The above has the following consequence: Of all triangles inscribed in a given triangle, that for which the sum of the squares of the sides is a minimum is the pedal triangle of the symmedian point [Johnson, p. 217].
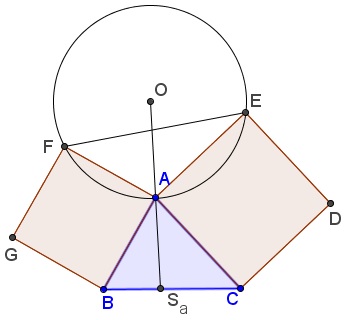
If squares $ABGF\;$ and $ACDE\;$ are constructed in the exterior of $\Delta ABC,\;$ then $AO,\;$ where $O\;$ is the center of circle $(AEF),\;$ is the symmedian in $\Delta ABC\;$ through $A.$
Let $MN\;$ be a transversal parallel to the side $BC\;$ of $\Delta ABC,\;$ with $M\;$ on $AB\;$ and $N\;$ $AC.\;$ The lines $BN\;$ and $CM\;$ meet at point $P.\;$ The circumcircles of triangles $BMP\;$ and $CNP\;$ meet at two distinct points $P\;$ and $Q.\;$

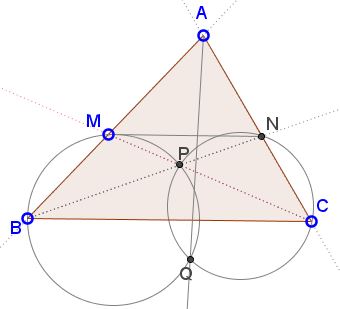
Then the line $AQ\;$ is the $A\text{-symmedian}\;$ of $\Delta ABC.$
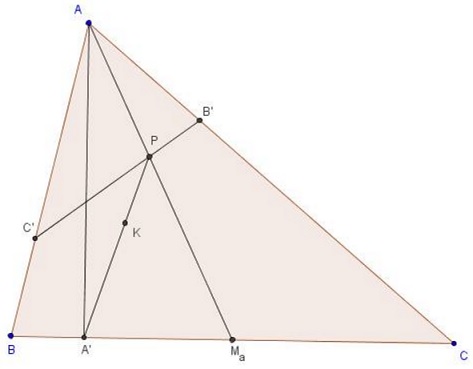
The Lemoine point is the intersection of the lines joining the midpoints of altitudes to the midpoints of sides, say the midpoint of the altitude from $A\;$ to the midpoint of side $BC.$
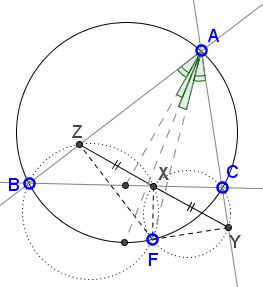
A point $F\;$ on the circumcircle of $\Delta ABC\;$ lies on a symmedian iff its projections on the sides of the triangles are equidistant:

The Lemoine point is also found to be the common point of the cevians in the orthic triangle defined by the intersection of the medians with the sides of the orthic triangle:

References

F. G.-M., Exercices de Géométrie, Éditions Jacques Gabay, sixiéme édition, 1991
R. Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, 1995.
R. A. Johnson, Advanced Euclidean Geometry (Modern Geometry), Dover, 1960
V. V. Prasolov, Essays On Numbers And Figures, AMS, 2000

Symmedian

70763154