An Inequality for the Cevians through Spieker Point via Brocard Angle
Problem
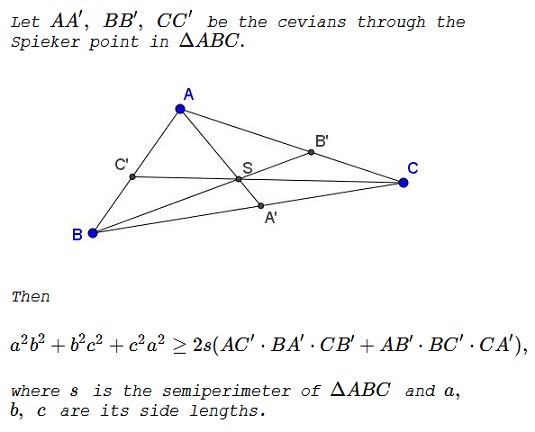
Solution 1
The Spieker point can be characterized in several ways. One of these is as a point where the three triangle's cleavers intersect. Thus, in particular,
$AB+BA'=AC+CA'=\displaystyle\frac{a+b+c}{2}=s,$
i.e., $BA'=\displaystyle\frac{a+b-c}{2}\,$ and $CA'=\displaystyle\frac{a-b+c}{2}.$
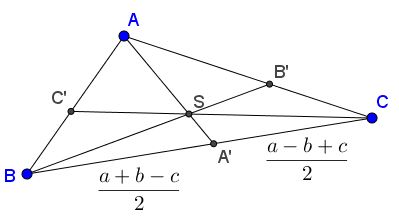
Similarly we can calculate the remaining four segments. To sum up,
$\displaystyle\begin{align}A'B&=B'A=\frac{a+b-c}{2},\\ A'C&=C'A=\frac{a-b+c}{2},\\ B'C&=C'B=\frac{-a+b+c}{2}. \end{align}$
There is a well known expression involving the Brocard angle $\omega\,$ of $\Delta ABC:$
$\displaystyle\sin^2\omega=\frac{(-a+b+c)(a-b+c)(a+b-c)(a+b+c)}{4(a^2b^2+b^2c^2+c^2a^2)}.$
Using that and $1\gt\sin^2\omega,\,$ we obtain
$\displaystyle\begin{align} 1&\gt\frac{2B'C\cdot 2C'A\cdot 2A'B\cdot 2s}{4(a^2b^2+b^2c^2+c^2a^2)}=\frac{4s\cdot B'C\cdot C'A\cdot A'B}{a^2b^2+b^2c^2+c^2a^2},\\ 1&\gt\frac{4s\cdot A'C\cdot C'B\cdot B'A}{a^2b^2+b^2c^2+c^2a^2}. \end{align}$
Summing up leads to the desired result.
Solution 2
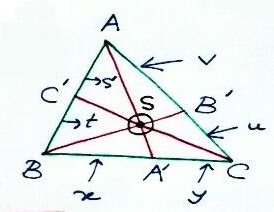
Using Ceva's theorem, with the notations illustrated by the diagram above,
$xus'=yvt.$
Substituting products $ab, bc, ca\,$ into $\displaystyle\sum_{cycl}x^2\ge\sum_{cycl}xy,\,$ and, in the above notations, we have:
$\displaystyle\begin{align} \sum_{cycl}a^2b^2 &\ge abc(a+b+c)\\ &=2s(x+y)(u+v)(s'+t)\\ &\ge 2s(2\sqrt{xy})(2\sqrt{uv})(2\sqrt{s't})\\ &=16s\sqrt{xus'}\sqrt{yvt}\\ &=16sxus'=16syvt\\ &=8s(xus'+yvt). \end{align}$
It follows that
$\displaystyle\sum_{cycl}a^2b^2\ge 8s(AC'\cdot BA'\cdot CB' + AB'\cdot BC'\cdot CA').$
Acknowledgment
The problem, with a solution (Solution 1), has been kindly communicated to me by Dan Sitaru. Solution 2 is by Soumava Chakraborty.
Soumava proof not only shows that the original estimate is off by a factor of 4, it also shows that estimate is valid for any three concurrent cevians, not just those through the Spieker point, which is, therefore, deservedly classified as a red herring.
What Is Red Herring
- On the Difference of Areas
- Area of the Union of Two Squares
- Circle through the Incenter
- Circle through the Incenter And Antiparallels
- Circle through the Circumcenter
- Inequality with Logarithms
- Breaking Chocolate Bars
- Circles through the Orthocenter
- 100 Grasshoppers on a Triangular Board
- Simultaneous Diameters in Concurrent Circles
- An Inequality from the 2015 Romanian TST
- Schur's Inequality
- Further Properties of Peculiar Circles
- Inequality with Csc And Sin
- Area Inequality in Trapezoid
- Triangles on HO
- From Angle Bisector to 120 degrees Angle
- A Case of Divergence
- An Inequality for the Cevians through Spieker Point via Brocard Angle
- An Inequality In Triangle and Without
- Problem 3 from the EGMO2017
- Mickey Might Be a Red Herring in the Mickey Mouse Theorem
- A Cyclic Inequality from the 6th IMO, 1964
- Three Complex Numbers Satisfy Fermat's Identity For Prime Powers
- Probability of Random Lines Crossing
- Planting Trees in a Row
- Two Colors - Three Points
- Inequalities in Triangle
- Padoa's Inequality
$(abc\ge (a+b-c)(b+c-a)(c+a-b))$
- Refinement of Padoa's Inequality $\left(\displaystyle \prod_{cycl}(a+b-c)\le 2\min_{cycl}\{a\cdot\frac{b^2c^2}{b^2+c^2}\}\le 2\max_{cycl}\{a\cdot\frac{b^2c^2}{b^2+c^2}\}\le abc\right)$
- Erdos-Mordell Inequality $(OA+OB+OC\ge 2(OP+OQ+OR) )$
- From Triangle Inequality to Inequality in Triangle $(\max\{A,B,C,D,E,F\}\le a^ab^bc^c)$
- Area Inequalities in Triangle $([\Delta NAP]\le\frac{1}{4}[\Delta ABC])$
- Area Inequality in Three Triangles $\displaystyle 2(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3})^2 \lt \sum_{cycl}a_1^2 + \sum_{cycl}a_2^2 + \sum_{cycl}a_3^2.$
- Area Inequality in Triangle II $([PBF]\le\frac{1}{6})$
- An Inequality in Triangle $(a^3b+b^3c+c^3a-a^2b^2-b^2c^2-c^2a^2\ge 0)$
- An Inequality in Triangle, II $(m_al_a+m_bl_b+m_cl_c\ge p^2)$
- An Inequality in Triangle III $\displaystyle\left(\frac{a(b+c)}{bc\cdot\cos^2\frac{A}{2}}+\frac{b(c+a)}{ca\cdot\cos^2\frac{B}{2}}+\frac{c(a+b)}{ab\cdot\cos^2\frac{C}{2}}\ge 8\right)$
- An Inequality in Triangle IV $\left(\begin{align}\sqrt{2}&\left[\sqrt{p(p-a)}+\sqrt{p(p-b)}+\sqrt{p(p-c)}\right]\\ &\le\sqrt{p^2-m_a^2}+\sqrt{p^2-m_b^2}+\sqrt{p^2-m_c^2}, \end{align}\right)$
- An Inequality in Triangle, V $(m_am_bm_c\ge r_ar_br_c)$
- An Inequality in Triangle, VI $\displaystyle\left(\frac{h_a\cdot h_b}{h_a+h_b}\right)\lt h_c\left(\frac{h_a\cdot h_b}{|h_a-h_b|}\right)$
- An Inequality in Triangle, VII $\displaystyle\left(\left(\sum_{cycl}\frac{m_a^2}{m_b^2}\right)\left(\sum_{cycl}x^2\right)+2\left(\sum_{cycl}\frac{m_a}{m_c}\right)\left(\sum_{cycl}xy\right)\ge 0\right)$
- An Inequality in Triangle, VIII $\displaystyle\left(\sum_{cycl}\frac{5a^2-b^2-c^2}{\sqrt{m_bm_c}}\le 4\sum_{cycl}m_a\right)$
- An Inequality in Triangle, IX $\displaystyle\left( 27\prod_{cycl}IA'\cdot HA''\le\frac{1}{27}\prod_{cycl}\ell_ah_a\right)$
- An Inequality in Triangle, X $\displaystyle\left(\frac{1}{r^2}\sum_{cycl}a^3\cos B\cos C\ge 16\left(\sum_{cycl}\sin A\right)\left(\sum_{cycl}\cos^2 A\right)\right)$
- An Inequality in Triangle XI $\left(3(a^2+b^2+c^2)\lt 4(am_c+bm_a+cm_b)\right)$
- Inequality In Triangle: Sides and Angle Bisectors $\left(\displaystyle a+b+c \ge \frac{2\sqrt{3}}{3}(l_a+l_b+l_c)\right)$
- Weitzenböck's inequality
$(a^2 + b^2 + c^2 \ge 4\sqrt{3}S)$
- Two Refinements of the Ionescu-Weitzenbock Inequality $(a^2+b^2+c^2\ge 2\sqrt{3}\max\{am_a,bm_b,cm_c\})$
- Another Refinement of the Ionescu-Weitzenbock Inequality $(\displaystyle a^2+b^2+c^2-4\sqrt{3}S\ge 2\sqrt{3}(m_a^2-h_a^2))$
- Early Refinement of the Ionescu-Weitzenbock Inequality $(\displaystyle a^2+b^2+c^2-(a-b)^2-(b-c)^2-(c-a)^2\ge 4\sqrt{3}S)$
- Weitzenbock by Sanchez $([ABC](1+\sqrt{3}]\le [ANBMCP])$
- An Inequality In Triangle That Involves the Four Basic Centers $\left(\displaystyle \sum_{cycl}(AH+2\cdot AI+3\cdot AO+4\cdot AG)\ge 60r\right)$
- An Inequality in Acute Triangle, Courtesy of Ceva's Theorem $\displaystyle\left(AB'\cdot BC'\cdot CA'+AB''\cdot BC''\cdot CA''+AB'''\cdot BC'''\cdot CA'''\le \frac{3}{8}abc\right)$
- Problem 4020 from Crux Mathematicorum $([MNP] \le [DEF])$
- A Two-Triangle Inequality $(a^2(-a'^2+b'^2+c'^2)+b^2(a'^2-b'^2+c'^2)+c^2(a'^2+b'^2-c'^2)\ge 16KK')$
- A Two-Triangle Inequality II $\left(\displaystyle\frac{a+b+c}{3\sqrt{3}R}\le\frac{\displaystyle\cos\frac{A}{2}+\cos\frac{B}{2}+\cos\frac{C}{2}}{\displaystyle\cos\frac{A'}{2}+\cos\frac{B'}{2}+\cos\frac{C'}{2}}\le\frac{3\sqrt{3}R'}{a'+b'+c'}\right)$
- Points on Incircle: Another Look $\left(\displaystyle 5r\le\frac{PA^2}{h_a}+\frac{PB^2}{h_b}+\frac{PC^2}{h_c}\le\frac{5}{2}R\right)$
- An All-Inclusive Inequality $\left(\displaystyle\frac{m_am_bm_c}{r_ar_br_c}+\frac{\ell_a\ell_b\ell_c}{h_ah_bh_c}\leq \frac{R}{r}\right)$
- An All-Inclusive Inequality II $\left(\displaystyle\left(\sum_{cycl}\sqrt{\frac{m_a}{\ell_a}}\right)\left(\sum_{cycl}\sqrt{\frac{m_a}{h_a}}\right)\le\frac{9R}{2r}\right)$
- Inequality with Roots, Squares and the Area $(\displaystyle \sqrt{2}(PA+PB+PC)\ge\sqrt{a^2+b^2+c^2+4\sqrt{3}S})$
- A One-Sided Inequality in Triangle $\left(\displaystyle BA'\cdot CB'\cdot AC' + BA''\cdot CB''\cdot AC'' + BA'''\cdot CB'''\cdot AC''' \lt \frac{3abc}{8}\right)$
- Dan Sitaru's Inequality with Tangents $(\displaystyle\sum_{cycl}\sqrt[3]{\tan A}\sqrt[3]{\tan B}(\sqrt[3]{\tan A}+\sqrt[3]{\tan B})\le 2\tan A\tan B\tan C)$
- Dan Sitaru's Inequality with Tangents II $(\displaystyle \sum_{cycl}\tan A\tan B + 45^{\circ}\le 2\tan^2A\tan^2B\tan^2C)$
- Dan Sitaru's Inequality with Roots and Powers $(\displaystyle (\sqrt{a}+\sqrt{b}+\sqrt{c})^4(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c})^6\ge 2^43^9S^2)$
- A Cyclic Inequality in Triangle $\left(\displaystyle\sum_{cycl}\frac{a^3(2s-a)}{b(2s-b)}\ge\frac{27a^2b^2c^2}{s^2}\right)$
- A Cyclic Inequality in Triangle II $\left(\displaystyle\sqrt{abc}\left(\frac{a^2}{\sqrt{b}}+\frac{b^2}{\sqrt{c}}+\frac{c^2}{\sqrt{a}}\right)^2\ge 16(\sqrt{a}+\sqrt{b}+\sqrt{c})S^2\right)$
- Inequality with Cubes and Cube Roots $(\displaystyle\sum_{cycl}(\sqrt[3]{a}+\sqrt[3]{b}-\sqrt[3]{c})^3\ge\sqrt[3]{3a}+\sqrt[3]{3b}+\sqrt[3]{3c}-2)$
- Tangent, Cotangent and Square Roots Inequality $(\displaystyle\left(\sum_{cycl}\sqrt{\cot A\cot B}\right)\left(\sum_{cycl}\sqrt{\tan A\cot B}\right)\ge 3\sqrt{3})$
- An Inequality with Sines $\left(\displaystyle \prod_{cycl}\left(\frac{2}{\sin A}-1\right)\ge\left(\frac{6}{\sin A+\sin B+\sin C}-1\right)^3\right)$
- An Inequality in Triangle, with Sines II $\left(\displaystyle \left(\sum_{cycl}\frac{\sin A}{\sin B}\right)\left(\sum_{cycl}\frac{\sin A}{\sin^2 B}\right)\left(\sum_{cycl}\frac{\sin A}{\sin^3 B}\right)\ge 24\sqrt{3}\right)$ $\left(\displaystyle\sin^22A+\sin^22B+\sin^22C\le\sin^2A+\sin^2B+\sin^2C\right)$
- An Inequality with Tangents and Cotangents $\left(\displaystyle\prod_{cycl}\left(\tan\frac{A}{2}\tan\frac{B}{2}+\cot\frac{A}{2}\cot\frac{B}{2}\right)\ge\frac{1000}{27}\right)$
- An Inequality with Sides and Medians $(2am_a\le bm_c+cm_b)$
- An Inequality in Triangle with Sides and Medians II $\left(\displaystyle 16\sum \Bigr(\frac{m_a}{m_c}+\frac{m_b}{m_c}\Bigr)^4\gt 81\Biggl(\Bigr(\frac{a}{m_a}\Bigr)^4+\Bigr(\frac{b}{m_b}\Bigr)^4+\Bigr(\frac{c}{m_c}\Bigr)^4\Biggl)\right)$
- An Inequality with Sin, Cos, Tan, Cot, and Some $(2S^2\displaystyle\sum_{cycl}(\sin A+\cos A+\tan A+\cot A)\gt 81\pi R^4\prod_{cycl}\cos A)$
- Leo Giugiuc's Second Lemma And Applications $(3(a+b)\gt 2(m_a+m_b))$
- An Inequality with Arctangents in Triangle $\left(\displaystyle\frac{a^3\cos^3A}{\arctan\frac{1}{2}}+\frac{b^3\cos^3B}{\arctan\frac{1}{5}}+\frac{c^3\cos^3C}{\arctan\frac{1}{8}}\ge\frac{32r^3s^3}{3\pi R^3}\right)$
- An Inequality in Triangle with Roots and Circumradius $(\displaystyle a\sqrt{b}+b\sqrt{c}+c\sqrt{a}\le 3R\sqrt{2s})$
- An Inequality for the Cevians through Circumcenter $\left(\displaystyle \frac{A_1O}{OA}+\frac{B_1O}{OB}+\frac{C_1O}{OC}=\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\ge\frac{3}{2}\right)$
- An Inequality with Powers of Six $(\displaystyle a^6+b^6+c^6\ge 8r^2s\sum_{cycl}\frac{a^5}{b^2-bc+c^2})$
- Adil Abdullayev's Inequality With Roots and Powers $\left(\displaystyle a^2+b^2+c^2\ge 4S\cdot\sqrt[4]{(a^2+b^2+c^2)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)}\right)$
- Marian Cucoanes' Inequality With Roots and Powers $\left(\displaystyle \small{a^2+b^2+c^2\ge 4S\cdot\sqrt{\frac{1}{2}(a^2+b^2+c^2)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)-\frac{3}{2}}}\right)$
- Marian Dinca's Inequality $\left(\displaystyle m_a\le\frac{s}{\sqrt{3}}\right)$
- An Inequality for the Cevians through Spieker Point via Brocard Angle $(a^2b^2+b^2c^2+c^2a^2 ≥ 2s(AC'\cdot BA'\cdot CB' + AB'\cdot BC'\cdot CA'))$
- Hung Nguyen Viet's Inequality with Radicals and Chebyshev $\left(\displaystyle\sum_{cycl}(a-\sqrt{bc})\sin\frac{A}{2}\ge 0\right)$
- An Inequality in Triangle, Mostly with the Medians $(\displaystyle \prod_{cycl}(5m_a+3m_b)(3m_a+5m_b)\lt 64\prod_{cycl}(2s+a)^2)$
- An Inequality in Triangle with Altitudes, Medians And Symmedians $\left(\displaystyle \frac{A_2A_3}{A_1A_2}\cdot\frac{B_2B_3}{B_1B_2}\cdot\frac{C_2C_3}{C_1C_2}\gt\prod_{cycl}\frac{(a+b-c)^2}{2a^2+2b^2-c^2}\right)$
- An Inequality with Altitudes and Medians $(\sqrt{3}\max (h_a,h_b,h_c)\ge s \ge \sqrt{3}\min (m_a,m_b,m_c))$
- An Inequality with Altitudes and Angle Bisectors $(\max (h_a,h_b,h_c)\ge \min (\ell_a,\ell_b,\ell_c))$
- Leo Giugiuc's Inequality for the Medians $(m_a+m_b+m_c\le\sqrt{3s^2+\frac{3}{4}[(a-b)^2+(b-c)^2+(c-a)^2]})$
- An Inequality in Triangle with Medians, Sides and Circumradius $(\displaystyle m_a\ge\frac{b^2+c^2}{4R})$
- An Inequality In Triangle with Sines of Half-Angles $\displaystyle\left( \sin\frac{A}{2}+\sin\frac{B}{2}+\sin\frac{C}{2}\le 2\sum_{cycl}\frac{a}{(\sqrt[3]{b}+\sqrt[3]{c})(\sqrt[3]{b^2}+\sqrt[3]{c^2})}\right)$
- An Inequality in Triangle with the Sines of Half-Angles and Cube Roots $\displaystyle\left( 2\sum_{cycl} \left(\frac{a}{b}+\frac{b}{a}\right)\sin^2 \frac{C}{2}\geq \sqrt[3]{abc}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\right)$
- An Inequality in Triangle with the Circumradius, Inradius and Angle Bisectors $(R+r\ge\min (\ell_a,\ell_b,\ell_c))$
- An Inequality in Triangle with Differences of the Medians $\displaystyle\left(\frac{8(m_a-m_b)(m_b-m_c)(m_c-m_a)}{(b-a)(c-b)(a-c)}>\frac{27abc}{(a+2s)(b+2s)(c+2s)}\right)$
- Problem 4087 from Crux Mathematicorum $( m_a(b+c)+2m_a^2\ge 4S\sin A)$
- An Inequality with Inradius and Circumradii $\left(\displaystyle (R_a+R_b+R_c)\left(\frac{R_a}{R_bR_c}+\frac{R_b}{R_cR_a}+\frac{R_c}{R_aR_b}\right)\ge 12-\frac{6r}{R}\right)$
- An Inequality in Triangle, with Integrals $\left(\displaystyle 4\sum_{cycl}\sin^2\frac{a}{2}+\pi\sum_{cycl}\int_{0}^{a}\cos (\sin x)dx\ge \pi^2\right)$
- An Inequality in Triangle, with Sines $\displaystyle\left(\prod_{cycl}\left(\frac{2}{\sin A}-1\right)\ge\left(\frac{6}{\sin A+\sin B+\sin C}-1\right)^3\right)$
- An Inequality in Triangle, with Sides and Sums $\left(\displaystyle \frac{a(2s-a)}{4(s-a)}+\frac{a(2s-b)}{4(s-b)}+\frac{a(2s-c)}{4(s-c)}\ge a+b+c\right)$
- An Inequality with a Variety of Circumradii $\left(\displaystyle \frac{R_a^2}{R_b}+\frac{R_b^2}{R_c}+\frac{R_c^2}{R_a}\geq 3R\right)$
- Dorin Marghidanu's Inequality with Maximum Side $\left(\displaystyle h_a \le \frac{p}{\sqrt{3}}\right)$
- An Inequality with Circumradii And Distances to the Vertices $\displaystyle\left(\frac{MB\cdot MC}{R_a}+\frac{MC\cdot MA}{R_b}+\frac{MA\cdot MB}{R_c}\le MA+MB+MC\right)$
- An inequality with Cosines and a Sine $\displaystyle\left(\cos A+4\cos B+4\sin\frac{C}{2}\le 9\cos\frac{\pi+B-C}{3}\right)$
- An inequality with Three Points $\displaystyle\left(\sum_{P\in\{O,I,G\}}\sum_{cycl}\left(\frac{[\Delta APB]}{[\Delta ABC]}+\frac{[\Delta ABC]}{[\Delta APB]}\right)^2\ge 100\right)$
- An Inequality with One Tangent and Six Sines $\left(\displaystyle \frac{\tan A}{\sin B+5\sin C}+\frac{\tan B}{\sin C+5\sin A}+\frac{\tan C}{\sin A+5\sin B}\gt\frac{1}{2}\right)$
- An Inequality with Tangents and Sides $\left(\displaystyle \frac{a^2}{\tan B+\tan C}+\frac{b^2}{\tan C+\tan A}+\frac{c^2}{\tan A+\tan B}\leq sR\right)$
- An Inequality with Sides, Altitudes, Angle Bisectors and Medians $\left(\displaystyle \left(\frac{h_b}{m_a}+\frac{h_c}{m_b}+\frac{h_a}{m_c}\right)\left(\frac{h_b}{\ell_a}+\frac{h_c}{\ell_b}+\frac{h_a}{\ell_c}\right)\ge\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)^2\right)$
- An Inequality of the Areas of Triangles Formed by Circumcenter And Orthocenter $\left(\displaystyle \sum_{cycl}\sqrt[n]{[\Delta OAB]}\ge\sum_{cycl}\sqrt[n]{[\Delta HAB]}\right)$
- An Inequality with Angle Trisectors $\left(\displaystyle \frac{AE}{AB}+\frac{AF}{AC}\lt 2\right)$
- An Inequality for Sides and Area $\left(\displaystyle \sum_{cycl}\frac{(a^2-ab+b^2)^2}{a^2+4ab+b^2}\ge\frac{2S}{\sqrt{3}}\right)$
- A Cyclic Inequality in Triangle for Integer Powers $\left(\displaystyle \sum_{cycl}\frac{a^{n+1}}{b+c-a}\ge\sum_{cycl}a^n\right)$
- R and r When G on Incircle $(8R\ge 25r)$
- An Inequality for Cevians And The Ratio of Circumradius and Inradius $\left(\displaystyle \frac{XB}{XY}\cdot\frac{YC}{YZ}\cdot\frac{ZA}{ZX}\le\frac{R}{2r}\right)$
- Centroid on the Incircle in Right Triangle $\left(648Rr\ge 25 (a^2+b^2+c^2)\right)$
- An Inequality with Cotangents And the Circumradius $\left(\displaystyle \sum_{cycl}a^2\cot B\cot C\le 4R^2\right)$
- An Inequality with Inradius and Excenters $\left(\displaystyle \sum_{cycl}\frac{1}{II_a^2}+\sum_{cycl}\frac{1}{I_aI_b^2}\le\frac{1}{4r^2}\right)$
- An Inequality with Inradius and Side Lengths $\left(\displaystyle \sum_{cycl}(b+c-a)^2\cdot\sum_{cycl}(b+c-a)^3\ge 2592\sqrt{3}r^5\right)$
- An Inequality with Exradii and an Altitude $\left(\displaystyle \sqrt{\frac{1}{r_b^2}+\frac{1}{r_c}+1}+\sqrt{\frac{1}{r_c^2}+\frac{1}{r_b}+1}\ge 2\sqrt{\frac{1}{h_a^2}+\frac{1}{h_a}+1}\right)$
- Leuenberger's Inequality for Medians, Inradius and Circumradius $\left(\displaystyle m_a+m_b+m_c\le 4R+r\right)$
- Adil Abdulayev's Inequality With Angles, Medians, Inradius and Circumradius $\left(\displaystyle \frac{A}{m_a}+\frac{B}{m_b}+\frac{C}{m_c}\le \frac{3\pi}{4R+r}\right)$
- An Inequality with Sides, Cosines, and Semiperimeter $\left(\displaystyle \sum_{cycl}a^2(b\cos B+c\cos C)\le \frac{8s^3}{9}\right)$
- Seyran Ibrahimov's Inequality $\left(\displaystyle \sqrt{3}s\cdot\sum_{cycl}m_a\le 20R^2+r^2\right)$
- An Inequality in Triangle, with Sides and Medians III $\left(\displaystyle \sum_{cycl}\frac{(m_b+m_c-m_a)^3}{m_a}\ge\frac{3}{4}(a^2+b^2+c^2)\right)$
- Leo Giugiuc's Inequality in Triangle, Solely with Cotangents $\left(\cot A +\cot B+\cot C\ge 2\sqrt{2}-1\right)$
- An Inequality in Triangle with Side Lengths and Circumradius $\left(\displaystyle\displaystyle\frac{ab}{\sqrt{a^2+b^2}}+\frac{bc}{\sqrt{b^2+c^2}}+\frac{ca}{\sqrt{c^2+a^2}}\le\frac{3\sqrt{6}R}{2}\right)$
- All Trigonometric Inequality in Triangle $\left(\displaystyle 3\sum_{cycl}\cos A\ge 2\sum_{cycl}\sin A\sin B\right)$
- An Inequality with Two Sets of Cevians $\left(\displaystyle \frac{27[A'B'C']}{[A''B''C'']}\leq \Bigr(\frac{BA'}{BA''}+\frac{CB'}{CB''}+\frac{AC'}{AC''}\Bigr)^3\right)$
- An Inequality with the Most Important Cevians $\left(\displaystyle \frac{m_am_bm_c}{h_ah_bh_c}\ge\frac{\ell_a^2+\ell_b^2+\ell_c^2}{\ell_a\ell_b+\ell_b\ell_c+\ell_c\ell_a}\right)$
- An Inequality in Triangle with a Constraint $(a\sqrt{2}\ge b+c)$
- Problem 11984 From the American Mathematical Monthly $\left(\displaystyle a^6+b^6+c^6\ge 5184\cdot r^6\right)$
- A Long Cyclic Inequality of Degree 4 $\left(\displaystyle 4\cdot\sum_{cycl}ab\cdot\sum_{cycl}a-\left(\sum_{cycl}a\right)^3\ge\frac{\displaystyle 3\sum_{cycl}ab\left[4\sum_{cycl}ab-\left(\sum_{cycl}a\right)^2\right]}{\displaystyle \sum_{cycl}a}\right)$
- An Inequality of Degree 3 with Inradius $\left(\displaystyle \sum_{cycl}(a+b-c)^3+24abc\ge 648\sqrt{3}r^3\right)$
- A Cyclic Inequality from the 6th IMO, 1964 $\left(\displaystyle \sum_{cycl}a^2(b+c-a)\le 3abc\right)$
- An Area Inequality in Right Triangle $\left(\displaystyle \frac{[\Delta ABD]+[\Delta ACE]}{[\Delta ADE]}\ge\sqrt{2}\right)$
- An Angle Inequality in Triangle with Perpendicular Medians $\left(\displaystyle \cos A\ge \frac{4}{5}\right)$
- An Inequality in Triangle form the 1996 APMO $\left(\sqrt{a+b-c}+\sqrt{b+c-a}+\sqrt{c+a-b}\le\sqrt{a}+\sqrt{b}+\sqrt{c}\right)$
- An Inequality in a Nonobtuse Triangle $\left(R\sqrt{2}\le h_a\right)$
- An Inequality in Triangle with Radicals, Semiperimeter and Inradius $\left(\displaystyle \sqrt{\frac{a+b}{s-b}}+ \sqrt{\frac{b+c}{s-c}} +\sqrt{\frac{c+a}{s-a}}\le \frac{\sqrt{a^2+b^2+c^2}}{r}\right)$
- Dan Sitaru's Inequality with Radicals and Cosines $\left(\displaystyle (a^2+b^2+c^2)^3\ge 6^3(abc)^2\cos A\cos B\cos C\right)$
- Lorian Saceanu's Cyclic Inequalities with Three Variables $\left(\displaystyle 2+\sum_{cycl}\frac{a}{b}\ge \sum_{cycl}\frac{a}{c}+2\frac{ab+bc+ca}{a^2+b^2+c^2}\right)$
- An Inequality for the Tangent to the Incircle $\left(\displaystyle DE\le\frac{1}{8}(AB+BC+CA)\right)$
- Lorian Saceanu's Sides And Angles Inequality $\left(\displaystyle \frac{\pi}{3}\le \frac{a\alpha + b\beta + c\gamma}{a+b+c}\le \arccos\left(\frac{r}{R}\right)\right)$
- An Inequality in Triangle with Radicals, Semiperimeter, Incenter and Inradius $\left(\displaystyle \frac{AI+BI+CI}{r}+3\ge\left(\sum_{cycl}\sqrt{s-a}\right)\left(\sum_{cycl}\frac{1}{\sqrt{s-a}}\right)\right)$
- An Inequality in Triangle for Side Lengths, Cycled in Two Ways $\left(\displaystyle 3\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}-1\right)\ge 2\left(\frac{b}{a}+\frac{a}{c}+\frac{c}{b}\right)\right)$
- Lorian Saceanu's Inequality for All Triangles $\left(\displaystyle \sin 2A+\sin 2B+\sin 2C\ge 4\sin 2A\cdot\sin 2B\cdot\sin 2C\right)$
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71547257
