A Special Triangle with a Line Through the Lemoine Point
Problem
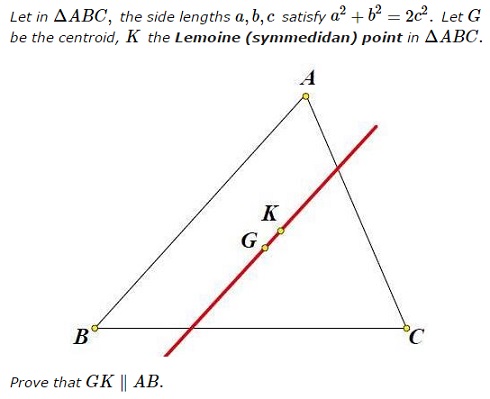
Proof 1
Let $a^2=x,\,b^2=y,\,c^2=z.\,$ We have $x+y=2z.\,$ We know that
$\displaystyle\overrightarrow{AK}=\frac{y\overrightarrow{AB}+z\overrightarrow{AC}}{x+y+z}=\frac{y\overrightarrow{AB}+z\overrightarrow{AC}}{3z}.$
Also, $\displaystyle\overrightarrow{AG}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{3},\,$ implying $\overrightarrow{GK}=\overrightarrow{AK}-\overrightarrow{AG}=\displaystyle\frac{(y-z)\overrightarrow{AB}}{3z},\,$ so that, indeed, $GK\parallel AB.$
Proof 2
In homogeneous barycentric coordinates, $G=1:1:1\,$ while $K=a^2:b^2:c^2.\,$ The equation of the side line $AB\,$ is $z=0.\,$ The equation of line $GK\,$ is
$\left|\begin{array}{ccc}\,x&y&z\\1&1&1\\a^2&b^2&c^2\end{array}\right|=(c^2-b^2)x+(a^2-c^2)y+(b^2-a^2)z=0.$
Since $c=\displaystyle\frac{a^2+b^2}{2},\,$ the equation of $GK\,$ is
$(a^2-b^2)x+(a^2-b^2)y+(b^2-a^2)z=0.$
The intersection of $GK\,$ with the line at infinity $x+y+z=0\,$ is $1:-1:0.\,$ This point also lies on $z=0,\,$ implying that the two lines intersect on the line at infinity. Hence, they are parallel.
Acknowledgment
Leo Giugiuc has kindly posted at the CutTheKnotMath facebook page the above problem, due to Kadir Altintas, with his solution (Proof 1) and the solution by the problem's author (Proof 2).
Symmedian
- All about Symmedians
- Symmedian and Antiparallel
- Symmedian and 2 Antiparallels
- Symmedian in a Right Triangle
- Nobbs' Points and Gergonne Line
- Three Tangents Theorem
- A Tangent in Concurrency
- Symmedian and the Tangents
- Ceva's Theorem
- Bride's Chair
- Star of David
- Concyclic Circumcenters: A Dynamic View
- Concyclic Circumcenters: A Sequel
- Steiner's Ratio Theorem
- Symmedian via Squares and a Circle
- Symmedian via Parallel Transversal and Two Circles
- Symmedian and the Simson
- Characterization of the Symmedian Point with Medians and Orthic Triangle
- A Special Triangle with a Line Through the Lemoine Point
|Contact| |Front page| |Contents| |Geometry|
Copyright © 1996-2018 Alexander Bogomolny71546914
