Seven Problems in Equilateral Triangle
Solution to Problems 5, 6, 7

Given an equilateral triangle $ABC$ with the base extended to twice its length: $AB'=AB.$ Let $B'E,$ $B'F$ be the tangents from $B'$ to $(ABC),$ with $E$ and $F$ being the points of tangency; $B'I$ (with $I$ on $(ABC))$ be the second tangent from $B'$ to the incircle of $\Delta ABC;$ $L$ the intersection of $B'I$ with $(ABC),$ $H$ the point of tangency with the incircle, $G$ the second point of intersection (besides $M$ - the midpoint of $AC).$

Problem 5

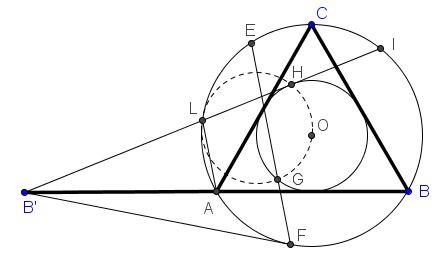
Problems 5 in equilateral triangle with one side extanded

Prove that the points $L,G,O,H$ are concyclic.

Problem 6

Problems 6 in equilateral triangle with one side extanded

Prove that the incircle and $(LGOH)$ have the same radius and the center of the latter lies on the incircle.

Problem 7

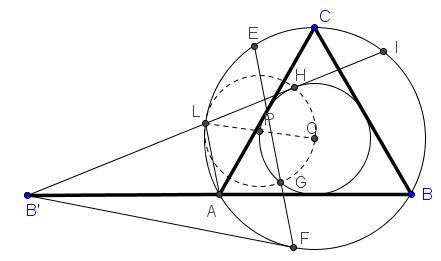
Problems 7 in equilateral triangle with one side extanded

Prove that the center of $(LGOH)$ is collinear with $O,L$.

Solution

Consider a reflection in $B'O:$ $L$ maps to $A,$ $M$ to $G,$ $H$ to $Q,$ the midpoint of $AB.$ Circle $(AOQ)$ is the reflection of $(LHO).$

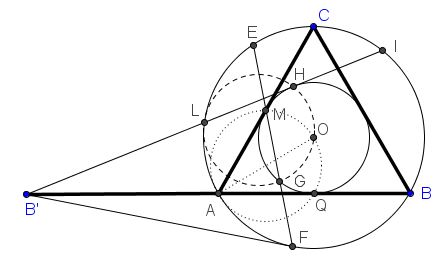
Problems 5, 6, 7 in equilateral triangle with one side extanded, solution

Since $OQ\perp AQ,$ $AO$ is a diameter of $(AOQ).$ The latter passes through $M$ because $OM\perp AM.$ It follows points $A, Q, O, M$ ar concyclic and so are their reflections $L,H,O,G.$

The diameter $AO$ is two thirds of the altitude in $\Delta ABC,$ whereas the radius of the incircle is one third of the latter. It follows that the circles have equal radii, implying, in particular, the center of one lies on the other.

Since the circumradius of $\Delta ABC$ equals two thirds of the altitude, circle $(AOQ)$ is tangent to the circumcircle at $A$ whereas its reflection $(LGOH)$ touches the circumcircle at $L.$

Extras

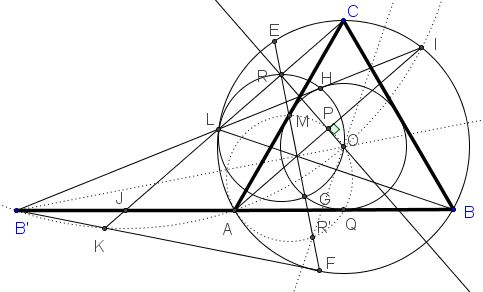
The intersection $R$ of $EF$ and $LI$ is also on $(LGOH).$ In addition, $OR\perp AI$ and, therefore, passes through the center of $(B'KAOI).$

Problems 5, 6, 7 in equilateral triangle with one side extanded, solution

Acknowledgment

The proof has been suggested by Machó Bónis at the CutTheKnotMath facebook page.

71536292