Reflections of the Orthocenter II

Vladimir Nikolin
an elementary school teacher from Serbia
April 23, 2010

Reflections of the orthocenter in the sidelines of a triangle lie on the circumcircle of the triangle.

Let H be the orthocenter in ΔABC. Let H' be the refection of H using line AB, and point D is the second end of the circumdiameter CD. M_c the midpoint of AB.

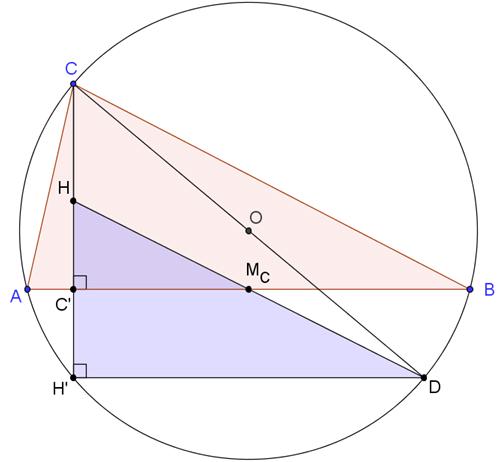
Since CD is a diameter, ∠CBD = 90° (as an inscribed angle subtended by a diameter), implying BD ⊥ BC. Also, AH being an altitude in ΔABC, is perpendicular to BC: AH ⊥ BC. Therefore, AH||BD.

Similarly, BH is an altitude (BH ⊥ AC) while ∠CAD = 90°. Therefore AD||BH.

The quadrilateral ADBH is a parallelogram. The diagonals AB and DH cross at their common midpoint which means that the midpoint M_c of AB lies on DH and, in addition, HM_c = M_cD.

Letting C' be the foot of the altitude CH, we have, by the construction, HC' = C'H'. In triangle DHH' C'M_c is the midline parallel to DH': C'M_c||DH'. And, since ∠BC'C = 90°, so too ∠DH'H = 90°. ∠DH'C (= ∠DH'H) is right and subtended by the circumdiameter CD so, by Thales' theorem H' lies on the circumcircle, as required.

Note: a different proof appears elsewhere.

The Orthocenter

1. Count the Orthocenters
2. Distance between the Orthocenter and Circumcenter
3. Circles through the Orthocenter
4. Reflections of the Orthocenter
5. CTK Wiki Math - Geometry - Reflections of the Orthocenter
6. Orthocenter and Three Equal Circles
7. A Proof of the Pythagorean theorem with Orthocenter and Right Isosceles Triangles
8. Reflections of a Line Through the Orthocenter
9. Equal Circles, Medial Triangle and Orthocenter
10. All About Altitudes
11. Orthocenters of Two Triangles Sharing Circumcenter and Base
12. Construction of a Triangle from Circumcenter, Orthocenter and Incenter
13. Reflections of the Orthocenter II
14. Circles On Cevians

|Contact| |Front page| |Contents| |Geometry| |Store|

Copyright © 1996-2012 Alexander Bogomolny