Trigonometry According to Ptolemy

Most of the modern mathematics has evolved in the past 3-4 centuries. However, some of the classic works by great mathematicians of Greece and Rome (and, of course, the Indian and Chinese ones) have endured over two millennia. There are theorems named after Thales, Archimedes, Euclid, Ptolemy, Apollonius, to name a few. It's often contended (but not every one agrees with that) that mathematics is a language. What is without doubt is that there is a mathematical language without which the development of mathematics would be impossible. Mathematics and its language evolved in tandem such that the famous authors might not be able to (at least immediately) recognize their eponymous theorems. As an example, what we now call Ptolemy's theorem:

Let a convex quadrilateral ABCD be inscribed in a circle. Then the sum of the products of the two pairs of opposite sides equals the product of its two diagonals.

Ptolemy's theorem

In other words $AD\cdot BC + AB\cdot CD = AC\cdot BD$

in Almagest was formulated in a way that many nowadays would have a difficulty to identify as such:

The rectangle contained by the diagonals of any quadrilateral inscribed in a circle is equal to the sum of rectangles contained by the pair of opposite sides.

So much of what can be found in the ancient sources would look differently when written in the modern language. Ptolemy's Almagest is in main an astronomical treatise where he developed and employed plane and spherical trigonometry. Following a Monthly article by J. Kocik and A. Solecki and Eli Maor's book, I'll present below some of the most basic highlights as it would have appeared in modern notations. These deal with triangle trigonometry and formulas for the trigonometric function in the notations that, according to Florian Cajori did not appear before the beginning of the seventeenth century.

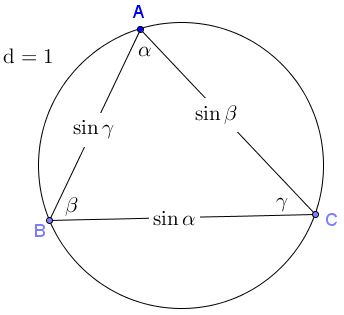
Ptolemy inscribes triangles in a unit circle, a circle with diameter $\mbox{d} = 1$ which makes the Law of Sines extremely simple and visually appealing:

The Law of Sines in the Unit Circle

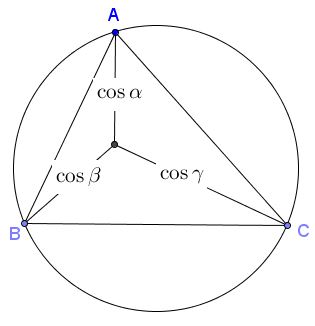
If we draw altitudes but only display their ears, we'll be able to identify cosines:

cosines in a triangle

Altitudes themselves are also easily expressed, e.g.,

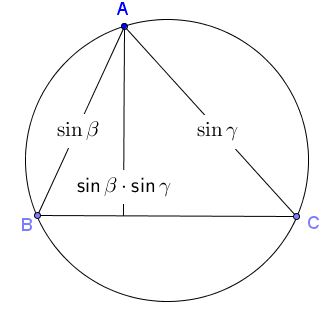
product of sines in a triangle

as are their stems:

product of cosines in a triangle

To better understand that you should consider the distribution of angles formed by the altitudes:

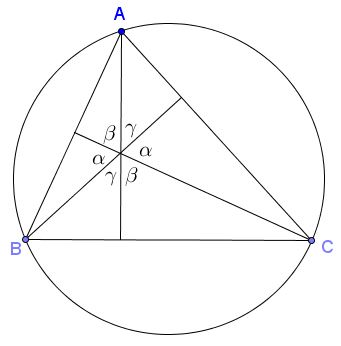
angles formed by the altitudes in a triangle

One (but not the only) way to convince yourself that this is true is to detect cyclic quadrilaterals, of which there are several, and to observe the angle which are pairwise opposite in one of them:

cyclic quadrilateral in a triangle

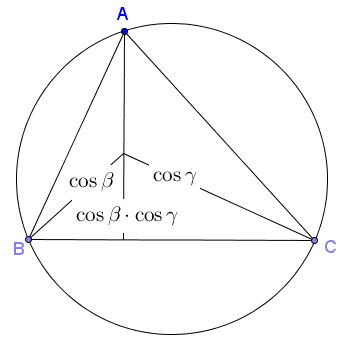
Then there is room for the mixed products:

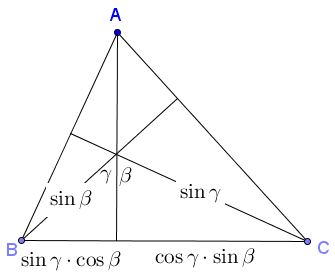
mixed products in a triangle

Comparing with an earlier diagram gives us immediately the addition formula for sine:

$\sin(\beta +\gamma )=\sin\alpha =\sin\beta\cdot\cos\gamma +\cos\beta\cdot\sin\gamma.$

This is not a difficult exercise to discover in the diagrams other trigonometric identities.

References

F. Cajori, A History of Mathematical Notations, Dover Publications, 1993
J. Kocik, A. Solecki, Disentangling a Triangle, Am Math Monthly 116 (March 2009), 228-237
E. Maor, Trigonometric Delights, Princeton University Press, 1998
Ptolemy, Almagest, Princeton University Press, 1998

Trigonometry

71537142