Characterization of the Symmedian Point with Medians and Orthic Triangle

Let $A'B'C'\;$ be the orthic triangle of $\Delta ABC,\;$ $M_a\;$ the midpoint of $BC\;$ and $P=AM_a\cap B'C'.\;$

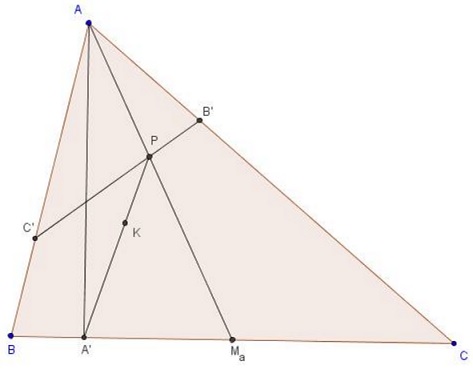
Nikolin's symmedian characterization

Then symmedian point $K\in A'P.$

Proof

We assume the triangle $ABC\;$ to be acute. The case of obtuse triangle is only slightly different.

Denote $a^2=x,\;$ $b^2=y,\;$ $c^2=z.\;$ We have

$\displaystyle\begin{align} \overrightarrow{AA'} &= \frac{(x+y-z)\overrightarrow{AB}+(x-y+z)\overrightarrow{AC}}{2x},\\ \overrightarrow{AB'} &= \frac{-x+y+z}{2y}\overrightarrow{AC},\\ \overrightarrow{AC'} &= \frac{-x+y+z}{2z}\overrightarrow{AB},\\ \overrightarrow{AK} &= \frac{y\overrightarrow{AB}+z\overrightarrow{AC}}{x+y+z}. \end{align}$

But $\overrightarrow{AP}=\alpha\overrightarrow{AB'}+(1-\alpha)\overrightarrow{AC'}\;$ and $\overrightarrow{AP}\;$ is proportional to $\overrightarrow{AB}+\overrightarrow{AC}.\;$ From here,

$\displaystyle\overrightarrow{AP}=\frac{-x+y+z}{2(y+z)}(\overrightarrow{AB}+\overrightarrow{AC}).\;$

Further

$\displaystyle\overrightarrow{KA'}=\overrightarrow{AA'}-\overrightarrow{AK}=\frac{(x^2+y^2-z^2)\overrightarrow{AB}+(x^2-y^2+z^2)\overrightarrow{AC}}{2x(x+y+z)}$

and

$\displaystyle\overrightarrow{PA'}=-\overrightarrow{AP}+\overrightarrow{AA'}=\frac{(x^2+y^2-z^2)\overrightarrow{AB}+(x^2-y^2+z^2)\overrightarrow{AC}}{2x(y+z)},$

which shows that the vectors $\overrightarrow{KA'}\;$ and $\overrightarrow{PA'}\;$ are collinear, proving the statement.

Acknowledgment

The statement has been devised by Vladimir Nikolin, the proof is due to Leo Giugiuc. I am grateful to Leo for helping me understand his elegant proof.

Symmedian

71543096