Morley's Theorem, a Proof
Brian Stonebridge (University of Bristol, UK)
Bill Millar
In Figure 1, the near trisectors of the internal angles at the vertices A, B, and C of a triangle meet in X, Y, and Z. Morley's theorem states that the triangle XYZ is equilateral. We give here a direct Euclidean proof.
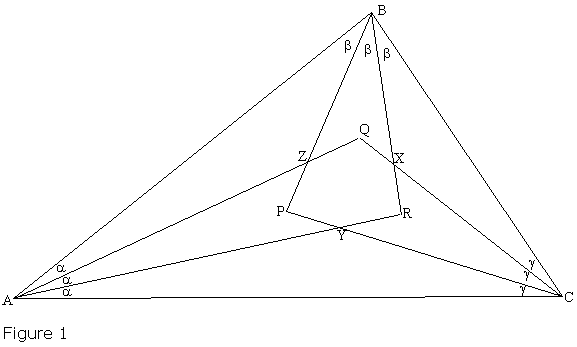
Let the far trisectors meet in P, Q, and R. The following proof that PX, QY, and RZ are concurrent is purely Euclidean; a stronger result can be proved using projective geometry. Figure 1 shows the angle values α, β, γ, implying α + β + γ = π/3, and ∠QXR = π - β - γ. Since Y is the incentre of ΔAQC, it follows that ∠ZQY = ∠XQY = β + π/6. The corresponding angles at R and P are γ + π/6, α + π/6.
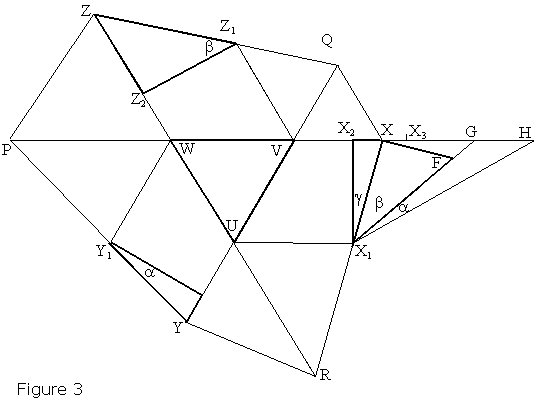
Assume PX, QY and RZ meet in pairs at U, V, and W. By transitivity, either U, V, W all coincide or are all distinct. We show that the assumption that the three points are distinct leads to a contradiction. Indeed, this might happen in two ways, as illustrated in Figures 2 and 3 (below.) We focus on the diagram of Figure 2, the other one being entirely analogous. Sum the angles of quadrilateral QURX, using the above results, to find ∠WUV = π/3. Hence ΔWUV is equilateral, with sides 2d, say. Thus we assume that
Choose X1 on QX such that UX1 is parallel to PX. Then the angles ZUQ, QUX1, X1UV all are π/3. Now choose X2 and X3 on PX such that ∠PX2X1 = π/2, and X1X3 is parallel to UV. These constructions imply ∠X2X1X = β (because in ΔQWX, ∠WQX = β + π/6 and ∠QWX = π/3 hence ∠QXW = π/2 - β) and X2X3 = d - from the choice of X3.
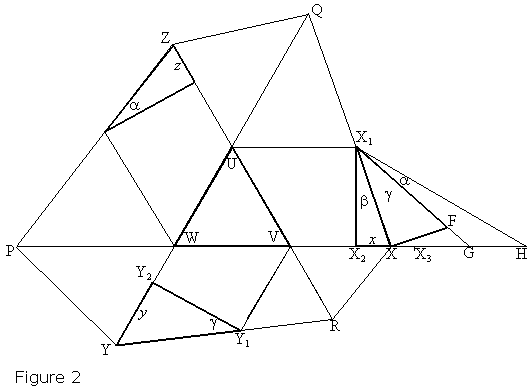
Denote X2X by x, then VX = VX3 - d + x. But VX3 = UX1 = UZ, from the congruence of triangles ZUQ and X1UQ. (These triangles are congruent since they have a common side UQ, the angles at Q are β + π/6, and the angles at U are π/3.) Hence
Similarly, defining y and z in the same way as for x,
| (3) | WY = VX - d + y, |
| (4) | UZ = WY - d + z. |
Adding equations (2)-(4) gives
Now extend the line PX to H, such that ∠X2X1H = π/3, and hence X2H = 3d. Indeed, in an equilateral triangle the ratio of the altitude to a half-side equals √3. In ΔUVW, this means that X1X2 = d × √3. In ΔX1X2H (which is a half of an equilateral triangle), we have X2H = X1X2 × √3. Multiplying through gives
| |
X2H | = X1X2 × √3 |
| | | = (d × √3) × √3 |
| | | = 3d. |
Choose G on X2H such that ∠XX1G = γ. Then ∠GX1H = α. Finally, choose F on X1G such that XF is normal to XX1. Then ΔXX1F and ΔY2Y1Y are similar. Since XX1 > X2X1 = Y2Y1, then XF > y. Because ∠XFG = π/2 + γ, it is the greatest angle in ΔXFG. Hence, by Euclid (I.19), XG is the longest side, so y < XG. Similarly, z < GH. Including x = X2X, it follows that x + y + z < 3d. This contradicts (5) and so the assumption d ≠ 0 was false. That is, PX, QY, and RZ are concurrent, with mutual angles of π/3.
Now complete the proof of Morley's Theorem. As was observed earlier, in Figure 2, UZ = UX1, so that ΔZUX1 is isosceles. Hence YQ, being the bisector at vertex U, is normal to the base ZX1. But X1 and X now the same point, so ZX is normal to YQ. Similarly, XY, YZ are normal to RZ, PX, implying that the ΔXYZ is equilateral.
- J.Conway's proof
- D. J. Newman's proof
- Bankoff's proof
- B. Bollobás' proof
- Another proof
- Nikos Dergiades' proof
- G. Zsolt Kiss' proof
- M. T. Naraniengar's proof
- Doodling and Miracles
- Morley's Pursuit of Incidence
- Lines, Circles and Beyond
- On Motivation and Understanding
- Bankoff's conundrum
- Of Looking and Seeing
- Morley's Redux and More, Alain Connes' proof
- An Unexpected Variant
- Proof by B. Stonebridge and B. Millar
- Proof by B. Stonebridge
- Proof by Nolan L Aljaddou
- Proof by Roger Smyth
Copyright © 1996-2009 Alexander Bogomolny
|
