An Inequality in Triangle, X
Problem
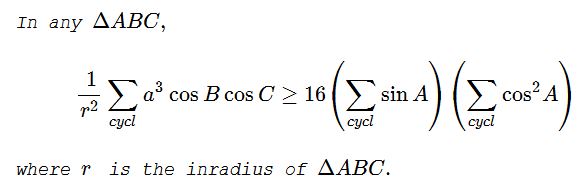
Proof
Since, by the Law of Sines, $\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}= 2R,\;$ where $R\;$ is the circumradius of $\Delta ABC,$
$\begin{align} \Delta &= \begin{vmatrix} a& b\cos C & c\cos B\\ b& c\cos A & a\cos C\\ c& a\cos B & b\cos A \end{vmatrix}\\ &=8R^3\begin{vmatrix} \sin A & \sin B\cos C & \sin C\cos B\\ \sin B & \sin C \cos A& \sin A\cos C\\ \sin C & \sin A\cos B & \sin B \cos A \end{vmatrix}\\ &=8R^3\begin{vmatrix} \sin A & \sin (B+C) & \sin C\cos B\\ \sin B & \sin (A+C) & \sin A\cos C\\ \sin C & \sin (A+B) & \sin B\cos A \end{vmatrix}\\ &=8R^3\begin{vmatrix} \sin A & \sin (\pi-A) & \sin C\cos B\\ \sin B & \sin (\pi-B) & \sin A \cos C\\ \sin C & \sin (\pi-C) & \sin B \cos A\\ \end{vmatrix}\\ &=8R^3\begin{vmatrix} \sin A & \sin A & \sin C\cos B\\ \sin B & \sin B & \sin A \cos C\\ \sin C & \sin C & \sin B \cos A\\ \end{vmatrix}\\ &=0. \end{align}$
On the other hand,
$\displaystyle\begin{align} 0=\Delta &=\begin{vmatrix} a& b\cos C & c\cos B\\ b& c\cos A & a\cos C\\ c& a\cos B & b\cos A \end{vmatrix}\\ &=abc\,\cos^2 A+abc\,\cos^2 C+abc\,\cos^2 A\\ &\;\;\;\;\;- c^3\,\cos A\cos B-a^3\,\cos B\cos C-b^3\,\cos A\cos C\\ &=abc\sum_{cycl} \cos^2 A-\sum_{cycl} a^3 \cos B\cos C\\ &=4RS\sum_{cycl} \cos^2 A-\sum_{cycl} a^3 \cos B\cos C, \end{align}$
where $S=[\Delta ABC]\;$ is the area of $\Delta ABC.$ (As is well known, $abc=4RS.)$
Further,
$\displaystyle\begin{align} \sum_{cycl} a^3 \cos B\cos C &=4RS\sum_{cycl} \cos^2 A\\ &=4Rrp\sum_{cycl} \cos^2 A\\ &=4Rr\cdot \frac{a+b+c}{2}\sum_{cycl} \cos^2 A \end{align}$
so that
$\displaystyle\begin{align} \frac{\displaystyle\sum_{cycl} a^3\cos B\cos C}{\displaystyle\sum_{cycl} \cos^2 A}&=2Rr(a+b+c)\\ &=2Rr\cdot 2R\cdot \sum_{cycl} \sin A\\ &=4R^2r\sum_{cycl} \sin A \end{align}$
Now using Euler's inequality $R\gt 2r,$
$\displaystyle\frac{\displaystyle\sum_{cycl} a^3\cos B\cos C}{\displaystyle\left(\sum_{cycl} \sin A\right)\left(\sum_{cycl} \cos^2 A\right)}= 4R^2r\ge 16r^3,$
which is the same as the required inequality.
Acknowledgment
The inequality and the solution have been kindly communicated to me by Dan Sitaru. It was published at the Romanian Mathematical Magazine.
- Inequalities in Triangle
- Padoa's Inequality
$(abc\ge (a+b-c)(b+c-a)(c+a-b))$
- Refinement of Padoa's Inequality $\left(\displaystyle \prod_{cycl}(a+b-c)\le 2\min_{cycl}\{a\cdot\frac{b^2c^2}{b^2+c^2}\}\le 2\max_{cycl}\{a\cdot\frac{b^2c^2}{b^2+c^2}\}\le abc\right)$
- Erdos-Mordell Inequality $(OA+OB+OC\ge 2(OP+OQ+OR) )$
- From Triangle Inequality to Inequality in Triangle $(\max\{A,B,C,D,E,F\}\le a^ab^bc^c)$
- Area Inequalities in Triangle $([\Delta NAP]\le\frac{1}{4}[\Delta ABC])$
- Area Inequality in Three Triangles $\displaystyle 2(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3})^2 \lt \sum_{cycl}a_1^2 + \sum_{cycl}a_2^2 + \sum_{cycl}a_3^2.$
- Area Inequality in Triangle II $([PBF]\le\frac{1}{6})$
- An Inequality in Triangle $(a^3b+b^3c+c^3a-a^2b^2-b^2c^2-c^2a^2\ge 0)$
- An Inequality in Triangle, II $(m_al_a+m_bl_b+m_cl_c\ge p^2)$
- An Inequality in Triangle III $\displaystyle\left(\frac{a(b+c)}{bc\cdot\cos^2\frac{A}{2}}+\frac{b(c+a)}{ca\cdot\cos^2\frac{B}{2}}+\frac{c(a+b)}{ab\cdot\cos^2\frac{C}{2}}\ge 8\right)$
- An Inequality in Triangle IV $\left(\begin{align}\sqrt{2}&\left[\sqrt{p(p-a)}+\sqrt{p(p-b)}+\sqrt{p(p-c)}\right]\\ &\le\sqrt{p^2-m_a^2}+\sqrt{p^2-m_b^2}+\sqrt{p^2-m_c^2}, \end{align}\right)$
- An Inequality in Triangle, V $(m_am_bm_c\ge r_ar_br_c)$
- An Inequality in Triangle, VI $\displaystyle\left(\frac{h_a\cdot h_b}{h_a+h_b}\right)\lt h_c\left(\frac{h_a\cdot h_b}{|h_a-h_b|}\right)$
- An Inequality in Triangle, VII $\displaystyle\left(\left(\sum_{cycl}\frac{m_a^2}{m_b^2}\right)\left(\sum_{cycl}x^2\right)+2\left(\sum_{cycl}\frac{m_a}{m_c}\right)\left(\sum_{cycl}xy\right)\ge 0\right)$
- An Inequality in Triangle, VIII $\displaystyle\left(\sum_{cycl}\frac{5a^2-b^2-c^2}{\sqrt{m_bm_c}}\le 4\sum_{cycl}m_a\right)$
- An Inequality in Triangle, IX $\displaystyle\left( 27\prod_{cycl}IA'\cdot HA''\le\frac{1}{27}\prod_{cycl}\ell_ah_a\right)$
- An Inequality in Triangle, X $\displaystyle\left(\frac{1}{r^2}\sum_{cycl}a^3\cos B\cos C\ge 16\left(\sum_{cycl}\sin A\right)\left(\sum_{cycl}\cos^2 A\right)\right)$
- An Inequality in Triangle XI $\left(3(a^2+b^2+c^2)\lt 4(am_c+bm_a+cm_b)\right)$
- Inequality In Triangle: Sides and Angle Bisectors $\left(\displaystyle a+b+c \ge \frac{2\sqrt{3}}{3}(l_a+l_b+l_c)\right)$
- Weitzenböck's inequality
$(a^2 + b^2 + c^2 \ge 4\sqrt{3}S)$
- Two Refinements of the Ionescu-Weitzenbock Inequality $(a^2+b^2+c^2\ge 2\sqrt{3}\max\{am_a,bm_b,cm_c\})$
- Another Refinement of the Ionescu-Weitzenbock Inequality $(\displaystyle a^2+b^2+c^2-4\sqrt{3}S\ge 2\sqrt{3}(m_a^2-h_a^2))$
- Early Refinement of the Ionescu-Weitzenbock Inequality $(\displaystyle a^2+b^2+c^2-(a-b)^2-(b-c)^2-(c-a)^2\ge 4\sqrt{3}S)$
- Weitzenbock by Sanchez $([ABC](1+\sqrt{3}]\le [ANBMCP])$
- An Inequality In Triangle That Involves the Four Basic Centers $\left(\displaystyle \sum_{cycl}(AH+2\cdot AI+3\cdot AO+4\cdot AG)\ge 60r\right)$
- An Inequality in Acute Triangle, Courtesy of Ceva's Theorem $\displaystyle\left(AB'\cdot BC'\cdot CA'+AB''\cdot BC''\cdot CA''+AB'''\cdot BC'''\cdot CA'''\le \frac{3}{8}abc\right)$
- Problem 4020 from Crux Mathematicorum $([MNP] \le [DEF])$
- A Two-Triangle Inequality $(a^2(-a'^2+b'^2+c'^2)+b^2(a'^2-b'^2+c'^2)+c^2(a'^2+b'^2-c'^2)\ge 16KK')$
- A Two-Triangle Inequality II $\left(\displaystyle\frac{a+b+c}{3\sqrt{3}R}\le\frac{\displaystyle\cos\frac{A}{2}+\cos\frac{B}{2}+\cos\frac{C}{2}}{\displaystyle\cos\frac{A'}{2}+\cos\frac{B'}{2}+\cos\frac{C'}{2}}\le\frac{3\sqrt{3}R'}{a'+b'+c'}\right)$
- Points on Incircle: Another Look $\left(\displaystyle 5r\le\frac{PA^2}{h_a}+\frac{PB^2}{h_b}+\frac{PC^2}{h_c}\le\frac{5}{2}R\right)$
- An All-Inclusive Inequality $\left(\displaystyle\frac{m_am_bm_c}{r_ar_br_c}+\frac{\ell_a\ell_b\ell_c}{h_ah_bh_c}\leq \frac{R}{r}\right)$
- An All-Inclusive Inequality II $\left(\displaystyle\left(\sum_{cycl}\sqrt{\frac{m_a}{\ell_a}}\right)\left(\sum_{cycl}\sqrt{\frac{m_a}{h_a}}\right)\le\frac{9R}{2r}\right)$
- Inequality with Roots, Squares and the Area $(\displaystyle \sqrt{2}(PA+PB+PC)\ge\sqrt{a^2+b^2+c^2+4\sqrt{3}S})$
- A One-Sided Inequality in Triangle $\left(\displaystyle BA'\cdot CB'\cdot AC' + BA''\cdot CB''\cdot AC'' + BA'''\cdot CB'''\cdot AC''' \lt \frac{3abc}{8}\right)$
- Dan Sitaru's Inequality with Tangents $(\displaystyle\sum_{cycl}\sqrt[3]{\tan A}\sqrt[3]{\tan B}(\sqrt[3]{\tan A}+\sqrt[3]{\tan B})\le 2\tan A\tan B\tan C)$
- Dan Sitaru's Inequality with Tangents II $(\displaystyle \sum_{cycl}\tan A\tan B + 45^{\circ}\le 2\tan^2A\tan^2B\tan^2C)$
- Dan Sitaru's Inequality with Roots and Powers $(\displaystyle (\sqrt{a}+\sqrt{b}+\sqrt{c})^4(\sqrt[3]{a}+\sqrt[3]{b}+\sqrt[3]{c})^6\ge 2^43^9S^2)$
- A Cyclic Inequality in Triangle $\left(\displaystyle\sum_{cycl}\frac{a^3(2s-a)}{b(2s-b)}\ge\frac{27a^2b^2c^2}{s^2}\right)$
- A Cyclic Inequality in Triangle II $\left(\displaystyle\sqrt{abc}\left(\frac{a^2}{\sqrt{b}}+\frac{b^2}{\sqrt{c}}+\frac{c^2}{\sqrt{a}}\right)^2\ge 16(\sqrt{a}+\sqrt{b}+\sqrt{c})S^2\right)$
- Inequality with Cubes and Cube Roots $(\displaystyle\sum_{cycl}(\sqrt[3]{a}+\sqrt[3]{b}-\sqrt[3]{c})^3\ge\sqrt[3]{3a}+\sqrt[3]{3b}+\sqrt[3]{3c}-2)$
- Tangent, Cotangent and Square Roots Inequality $(\displaystyle\left(\sum_{cycl}\sqrt{\cot A\cot B}\right)\left(\sum_{cycl}\sqrt{\tan A\cot B}\right)\ge 3\sqrt{3})$
- An Inequality with Sines $\left(\displaystyle \prod_{cycl}\left(\frac{2}{\sin A}-1\right)\ge\left(\frac{6}{\sin A+\sin B+\sin C}-1\right)^3\right)$
- An Inequality in Triangle, with Sines II $\left(\displaystyle \left(\sum_{cycl}\frac{\sin A}{\sin B}\right)\left(\sum_{cycl}\frac{\sin A}{\sin^2 B}\right)\left(\sum_{cycl}\frac{\sin A}{\sin^3 B}\right)\ge 24\sqrt{3}\right)$ $\left(\displaystyle\sin^22A+\sin^22B+\sin^22C\le\sin^2A+\sin^2B+\sin^2C\right)$
- An Inequality with Tangents and Cotangents $\left(\displaystyle\prod_{cycl}\left(\tan\frac{A}{2}\tan\frac{B}{2}+\cot\frac{A}{2}\cot\frac{B}{2}\right)\ge\frac{1000}{27}\right)$
- An Inequality with Sides and Medians $(2am_a\le bm_c+cm_b)$
- An Inequality in Triangle with Sides and Medians II $\left(\displaystyle 16\sum \Bigr(\frac{m_a}{m_c}+\frac{m_b}{m_c}\Bigr)^4\gt 81\Biggl(\Bigr(\frac{a}{m_a}\Bigr)^4+\Bigr(\frac{b}{m_b}\Bigr)^4+\Bigr(\frac{c}{m_c}\Bigr)^4\Biggl)\right)$
- An Inequality with Sin, Cos, Tan, Cot, and Some $(2S^2\displaystyle\sum_{cycl}(\sin A+\cos A+\tan A+\cot A)\gt 81\pi R^4\prod_{cycl}\cos A)$
- Leo Giugiuc's Second Lemma And Applications $(3(a+b)\gt 2(m_a+m_b))$
- An Inequality with Arctangents in Triangle $\left(\displaystyle\frac{a^3\cos^3A}{\arctan\frac{1}{2}}+\frac{b^3\cos^3B}{\arctan\frac{1}{5}}+\frac{c^3\cos^3C}{\arctan\frac{1}{8}}\ge\frac{32r^3s^3}{3\pi R^3}\right)$
- An Inequality in Triangle with Roots and Circumradius $(\displaystyle a\sqrt{b}+b\sqrt{c}+c\sqrt{a}\le 3R\sqrt{2s})$
- An Inequality for the Cevians through Circumcenter $\left(\displaystyle \frac{A_1O}{OA}+\frac{B_1O}{OB}+\frac{C_1O}{OC}=\frac{x}{y+z}+\frac{y}{z+x}+\frac{z}{x+y}\ge\frac{3}{2}\right)$
- An Inequality with Powers of Six $(\displaystyle a^6+b^6+c^6\ge 8r^2s\sum_{cycl}\frac{a^5}{b^2-bc+c^2})$
- Adil Abdullayev's Inequality With Roots and Powers $\left(\displaystyle a^2+b^2+c^2\ge 4S\cdot\sqrt[4]{(a^2+b^2+c^2)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)}\right)$
- Marian Cucoanes' Inequality With Roots and Powers $\left(\displaystyle \small{a^2+b^2+c^2\ge 4S\cdot\sqrt{\frac{1}{2}(a^2+b^2+c^2)\left(\frac{1}{a^2}+\frac{1}{b^2}+\frac{1}{c^2}\right)-\frac{3}{2}}}\right)$
- Marian Dinca's Inequality $\left(\displaystyle m_a\le\frac{s}{\sqrt{3}}\right)$
- An Inequality for the Cevians through Spieker Point via Brocard Angle $(a^2b^2+b^2c^2+c^2a^2 ≥ 2s(AC'\cdot BA'\cdot CB' + AB'\cdot BC'\cdot CA'))$
- Hung Nguyen Viet's Inequality with Radicals and Chebyshev $\left(\displaystyle\sum_{cycl}(a-\sqrt{bc})\sin\frac{A}{2}\ge 0\right)$
- An Inequality in Triangle, Mostly with the Medians $(\displaystyle \prod_{cycl}(5m_a+3m_b)(3m_a+5m_b)\lt 64\prod_{cycl}(2s+a)^2)$
- An Inequality in Triangle with Altitudes, Medians And Symmedians $\left(\displaystyle \frac{A_2A_3}{A_1A_2}\cdot\frac{B_2B_3}{B_1B_2}\cdot\frac{C_2C_3}{C_1C_2}\gt\prod_{cycl}\frac{(a+b-c)^2}{2a^2+2b^2-c^2}\right)$
- An Inequality with Altitudes and Medians $(\sqrt{3}\max (h_a,h_b,h_c)\ge s \ge \sqrt{3}\min (m_a,m_b,m_c))$
- An Inequality with Altitudes and Angle Bisectors $(\max (h_a,h_b,h_c)\ge \min (\ell_a,\ell_b,\ell_c))$
- Leo Giugiuc's Inequality for the Medians $(m_a+m_b+m_c\le\sqrt{3s^2+\frac{3}{4}[(a-b)^2+(b-c)^2+(c-a)^2]})$
- An Inequality in Triangle with Medians, Sides and Circumradius $(\displaystyle m_a\ge\frac{b^2+c^2}{4R})$
- An Inequality In Triangle with Sines of Half-Angles $\displaystyle\left( \sin\frac{A}{2}+\sin\frac{B}{2}+\sin\frac{C}{2}\le 2\sum_{cycl}\frac{a}{(\sqrt[3]{b}+\sqrt[3]{c})(\sqrt[3]{b^2}+\sqrt[3]{c^2})}\right)$
- An Inequality in Triangle with the Sines of Half-Angles and Cube Roots $\displaystyle\left( 2\sum_{cycl} \left(\frac{a}{b}+\frac{b}{a}\right)\sin^2 \frac{C}{2}\geq \sqrt[3]{abc}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\right)$
- An Inequality in Triangle with the Circumradius, Inradius and Angle Bisectors $(R+r\ge\min (\ell_a,\ell_b,\ell_c))$
- An Inequality in Triangle with Differences of the Medians $\displaystyle\left(\frac{8(m_a-m_b)(m_b-m_c)(m_c-m_a)}{(b-a)(c-b)(a-c)}>\frac{27abc}{(a+2s)(b+2s)(c+2s)}\right)$
- Problem 4087 from Crux Mathematicorum $( m_a(b+c)+2m_a^2\ge 4S\sin A)$
- An Inequality with Inradius and Circumradii $\left(\displaystyle (R_a+R_b+R_c)\left(\frac{R_a}{R_bR_c}+\frac{R_b}{R_cR_a}+\frac{R_c}{R_aR_b}\right)\ge 12-\frac{6r}{R}\right)$
- An Inequality in Triangle, with Integrals $\left(\displaystyle 4\sum_{cycl}\sin^2\frac{a}{2}+\pi\sum_{cycl}\int_{0}^{a}\cos (\sin x)dx\ge \pi^2\right)$
- An Inequality in Triangle, with Sines $\displaystyle\left(\prod_{cycl}\left(\frac{2}{\sin A}-1\right)\ge\left(\frac{6}{\sin A+\sin B+\sin C}-1\right)^3\right)$
- An Inequality in Triangle, with Sides and Sums $\left(\displaystyle \frac{a(2s-a)}{4(s-a)}+\frac{a(2s-b)}{4(s-b)}+\frac{a(2s-c)}{4(s-c)}\ge a+b+c\right)$
- An Inequality with a Variety of Circumradii $\left(\displaystyle \frac{R_a^2}{R_b}+\frac{R_b^2}{R_c}+\frac{R_c^2}{R_a}\geq 3R\right)$
- Dorin Marghidanu's Inequality with Maximum Side $\left(\displaystyle h_a \le \frac{p}{\sqrt{3}}\right)$
- An Inequality with Circumradii And Distances to the Vertices $\displaystyle\left(\frac{MB\cdot MC}{R_a}+\frac{MC\cdot MA}{R_b}+\frac{MA\cdot MB}{R_c}\le MA+MB+MC\right)$
- An inequality with Cosines and a Sine $\displaystyle\left(\cos A+4\cos B+4\sin\frac{C}{2}\le 9\cos\frac{\pi+B-C}{3}\right)$
- An inequality with Three Points $\displaystyle\left(\sum_{P\in\{O,I,G\}}\sum_{cycl}\left(\frac{[\Delta APB]}{[\Delta ABC]}+\frac{[\Delta ABC]}{[\Delta APB]}\right)^2\ge 100\right)$
- An Inequality with One Tangent and Six Sines $\left(\displaystyle \frac{\tan A}{\sin B+5\sin C}+\frac{\tan B}{\sin C+5\sin A}+\frac{\tan C}{\sin A+5\sin B}\gt\frac{1}{2}\right)$
- An Inequality with Tangents and Sides $\left(\displaystyle \frac{a^2}{\tan B+\tan C}+\frac{b^2}{\tan C+\tan A}+\frac{c^2}{\tan A+\tan B}\leq sR\right)$
- An Inequality with Sides, Altitudes, Angle Bisectors and Medians $\left(\displaystyle \left(\frac{h_b}{m_a}+\frac{h_c}{m_b}+\frac{h_a}{m_c}\right)\left(\frac{h_b}{\ell_a}+\frac{h_c}{\ell_b}+\frac{h_a}{\ell_c}\right)\ge\left(\frac{b}{a}+\frac{c}{b}+\frac{a}{c}\right)^2\right)$
- An Inequality of the Areas of Triangles Formed by Circumcenter And Orthocenter $\left(\displaystyle \sum_{cycl}\sqrt[n]{[\Delta OAB]}\ge\sum_{cycl}\sqrt[n]{[\Delta HAB]}\right)$
- An Inequality with Angle Trisectors $\left(\displaystyle \frac{AE}{AB}+\frac{AF}{AC}\lt 2\right)$
- An Inequality for Sides and Area $\left(\displaystyle \sum_{cycl}\frac{(a^2-ab+b^2)^2}{a^2+4ab+b^2}\ge\frac{2S}{\sqrt{3}}\right)$
- A Cyclic Inequality in Triangle for Integer Powers $\left(\displaystyle \sum_{cycl}\frac{a^{n+1}}{b+c-a}\ge\sum_{cycl}a^n\right)$
- R and r When G on Incircle $(8R\ge 25r)$
- An Inequality for Cevians And The Ratio of Circumradius and Inradius $\left(\displaystyle \frac{XB}{XY}\cdot\frac{YC}{YZ}\cdot\frac{ZA}{ZX}\le\frac{R}{2r}\right)$
- Centroid on the Incircle in Right Triangle $\left(648Rr\ge 25 (a^2+b^2+c^2)\right)$
- An Inequality with Cotangents And the Circumradius $\left(\displaystyle \sum_{cycl}a^2\cot B\cot C\le 4R^2\right)$
- An Inequality with Inradius and Excenters $\left(\displaystyle \sum_{cycl}\frac{1}{II_a^2}+\sum_{cycl}\frac{1}{I_aI_b^2}\le\frac{1}{4r^2}\right)$
- An Inequality with Inradius and Side Lengths $\left(\displaystyle \sum_{cycl}(b+c-a)^2\cdot\sum_{cycl}(b+c-a)^3\ge 2592\sqrt{3}r^5\right)$
- An Inequality with Exradii and an Altitude $\left(\displaystyle \sqrt{\frac{1}{r_b^2}+\frac{1}{r_c}+1}+\sqrt{\frac{1}{r_c^2}+\frac{1}{r_b}+1}\ge 2\sqrt{\frac{1}{h_a^2}+\frac{1}{h_a}+1}\right)$
- Leuenberger's Inequality for Medians, Inradius and Circumradius $\left(\displaystyle m_a+m_b+m_c\le 4R+r\right)$
- Adil Abdulayev's Inequality With Angles, Medians, Inradius and Circumradius $\left(\displaystyle \frac{A}{m_a}+\frac{B}{m_b}+\frac{C}{m_c}\le \frac{3\pi}{4R+r}\right)$
- An Inequality with Sides, Cosines, and Semiperimeter $\left(\displaystyle \sum_{cycl}a^2(b\cos B+c\cos C)\le \frac{8s^3}{9}\right)$
- Seyran Ibrahimov's Inequality $\left(\displaystyle \sqrt{3}s\cdot\sum_{cycl}m_a\le 20R^2+r^2\right)$
- An Inequality in Triangle, with Sides and Medians III $\left(\displaystyle \sum_{cycl}\frac{(m_b+m_c-m_a)^3}{m_a}\ge\frac{3}{4}(a^2+b^2+c^2)\right)$
- Leo Giugiuc's Inequality in Triangle, Solely with Cotangents $\left(\cot A +\cot B+\cot C\ge 2\sqrt{2}-1\right)$
- An Inequality in Triangle with Side Lengths and Circumradius $\left(\displaystyle\displaystyle\frac{ab}{\sqrt{a^2+b^2}}+\frac{bc}{\sqrt{b^2+c^2}}+\frac{ca}{\sqrt{c^2+a^2}}\le\frac{3\sqrt{6}R}{2}\right)$
- All Trigonometric Inequality in Triangle $\left(\displaystyle 3\sum_{cycl}\cos A\ge 2\sum_{cycl}\sin A\sin B\right)$
- An Inequality with Two Sets of Cevians $\left(\displaystyle \frac{27[A'B'C']}{[A''B''C'']}\leq \Bigr(\frac{BA'}{BA''}+\frac{CB'}{CB''}+\frac{AC'}{AC''}\Bigr)^3\right)$
- An Inequality with the Most Important Cevians $\left(\displaystyle \frac{m_am_bm_c}{h_ah_bh_c}\ge\frac{\ell_a^2+\ell_b^2+\ell_c^2}{\ell_a\ell_b+\ell_b\ell_c+\ell_c\ell_a}\right)$
- An Inequality in Triangle with a Constraint $(a\sqrt{2}\ge b+c)$
- Problem 11984 From the American Mathematical Monthly $\left(\displaystyle a^6+b^6+c^6\ge 5184\cdot r^6\right)$
- A Long Cyclic Inequality of Degree 4 $\left(\displaystyle 4\cdot\sum_{cycl}ab\cdot\sum_{cycl}a-\left(\sum_{cycl}a\right)^3\ge\frac{\displaystyle 3\sum_{cycl}ab\left[4\sum_{cycl}ab-\left(\sum_{cycl}a\right)^2\right]}{\displaystyle \sum_{cycl}a}\right)$
- An Inequality of Degree 3 with Inradius $\left(\displaystyle \sum_{cycl}(a+b-c)^3+24abc\ge 648\sqrt{3}r^3\right)$
- A Cyclic Inequality from the 6th IMO, 1964 $\left(\displaystyle \sum_{cycl}a^2(b+c-a)\le 3abc\right)$
- An Area Inequality in Right Triangle $\left(\displaystyle \frac{[\Delta ABD]+[\Delta ACE]}{[\Delta ADE]}\ge\sqrt{2}\right)$
- An Angle Inequality in Triangle with Perpendicular Medians $\left(\displaystyle \cos A\ge \frac{4}{5}\right)$
- An Inequality in Triangle form the 1996 APMO $\left(\sqrt{a+b-c}+\sqrt{b+c-a}+\sqrt{c+a-b}\le\sqrt{a}+\sqrt{b}+\sqrt{c}\right)$
- An Inequality in a Nonobtuse Triangle $\left(R\sqrt{2}\le h_a\right)$
- An Inequality in Triangle with Radicals, Semiperimeter and Inradius $\left(\displaystyle \sqrt{\frac{a+b}{s-b}}+ \sqrt{\frac{b+c}{s-c}} +\sqrt{\frac{c+a}{s-a}}\le \frac{\sqrt{a^2+b^2+c^2}}{r}\right)$
- Dan Sitaru's Inequality with Radicals and Cosines $\left(\displaystyle (a^2+b^2+c^2)^3\ge 6^3(abc)^2\cos A\cos B\cos C\right)$
- Lorian Saceanu's Cyclic Inequalities with Three Variables $\left(\displaystyle 2+\sum_{cycl}\frac{a}{b}\ge \sum_{cycl}\frac{a}{c}+2\frac{ab+bc+ca}{a^2+b^2+c^2}\right)$
- An Inequality for the Tangent to the Incircle $\left(\displaystyle DE\le\frac{1}{8}(AB+BC+CA)\right)$
- Lorian Saceanu's Sides And Angles Inequality $\left(\displaystyle \frac{\pi}{3}\le \frac{a\alpha + b\beta + c\gamma}{a+b+c}\le \arccos\left(\frac{r}{R}\right)\right)$
- An Inequality in Triangle with Radicals, Semiperimeter, Incenter and Inradius $\left(\displaystyle \frac{AI+BI+CI}{r}+3\ge\left(\sum_{cycl}\sqrt{s-a}\right)\left(\sum_{cycl}\frac{1}{\sqrt{s-a}}\right)\right)$
- An Inequality in Triangle for Side Lengths, Cycled in Two Ways $\left(\displaystyle 3\left(\frac{a}{b}+\frac{b}{c}+\frac{c}{a}-1\right)\ge 2\left(\frac{b}{a}+\frac{a}{c}+\frac{c}{b}\right)\right)$
- Lorian Saceanu's Inequality for All Triangles $\left(\displaystyle \sin 2A+\sin 2B+\sin 2C\ge 4\sin 2A\cdot\sin 2B\cdot\sin 2C\right)$
|Contact| |Front page| |Contents| |Inequalities| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
71535083