The 80-80-20 Triangle Problem
A Curious Partition
Inverse Problem
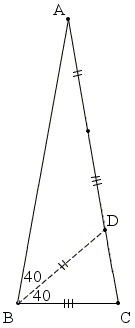
In ΔABC, ∠B = 80°. The bisector of angle B meets AC in D such that
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
In ΔABC, ∠B = 80°. The bisector of angle B meets AC in D such that
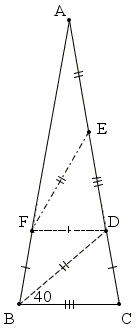
Let F on AB be such that DF||BC. Then
∠BDF = ∠CBD = ∠DBF = 40°,
making, in particular, ΔBDF isosceles:
BF = DF = CD.
Next, since DF||BC, ∠ADF = ∠ACB = ∠DCB. Let E be on AD such that
But we know that AD = BC + BD and DE = BC. This yields AE = BD so that ΔAEF is isosceles:
∠DEF = ∠CBD = 40°, implying ∠FAE = ∠EAF = 20°. Finally, in ΔABC,
This problem is an inverse to another one related to the 80-80-20 triangle.
Note: the above solution has been observed to contain a logical flaw; an implicit assumption made in the proof happened to be equivalent to the statement of the problem. The corrected solution appears elsewhere.
|Contact| |Front page| |Contents| |Geometry| |Up|
Copyright © 1996-2018 Alexander Bogomolny
71548168
